
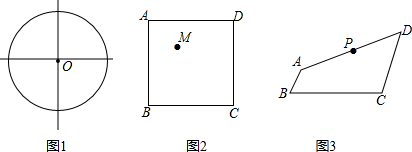
分析 (1)通过对图(1)的分析,根据中心对称图形性质,连接正方形对角线AB、CD,相较于点O,连接OM交正方形边于点E、F,过点O做EF的垂线,交正方形边于点G、H,则直线EF、GH即为所求.
(2)存在,当BQ=CD=b时,PQ将四边形ABCD的面积二等分.利用全等三角形△ABP≌△DEP性质,证明S△BPC=S△EPC,利用面积分析,即可得出BQ=b.
解答 解:(1)通过对图(1)的分析,得出以下结论,
过中心对称图形的对称中心任何一条直线可以平分图形面积.
如下图:连接正方形对角线AB、CD,相较于点O,
连接OM交正方形边于点E、F,
过点O做EF的垂线,交正方形边于点G、H,
则直线EF、GH即为所求.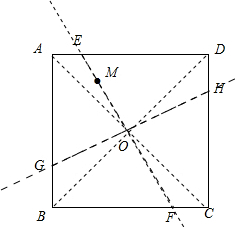
(2)存在,当BQ=CD=b时,PQ将四边形ABCD的面积二等分.
如下图,连接BP并延长交CD的延长线于点E,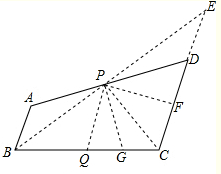
∵AB∥CD,
∴∠A=∠EDP,
在△ABP和△DEP中
$\left\{\begin{array}{l}{∠A=∠EDP\\;}\\{AP=DP}\\{∠APB=∠DPE}\end{array}\right.$,
△ABP≌△DEP(ASA),
∴BP=EP,
连接CP,
∵△BPC的边BP和△EPC的边EP上的高相等,
又∵BP=EP,
∴S△BPC=S△EPC,
作PF⊥CD,PG⊥BC,则BC=AB+CD=DE+CD=CE,
由三角形面积公式得:PF=PG,
在CB上截取CQ=DE=AB=a,则S△CQP=S△DEP=S△ABP
∴S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP
即:S四边形ABQP=S四边形CDPQ,
∵BC=AB+CD=a+b,
∴BQ=b,
∴当BQ=b时,直线PQ将四边形ABCD的面积分成相等的两部分.
点评 题目考查了圆及其它图形二等分面积,通过对图形性质的分析,考察学生的观察能力、分析能力和解决问题的能力,题目整体较难,对学生整体能力要求较高.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
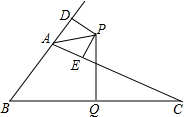 如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.若AB=6cm,AC=10cm,则AD=2cm.
如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.若AB=6cm,AC=10cm,则AD=2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
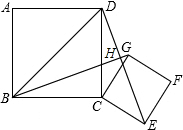 将边长为$\sqrt{5}$的正方形ABCD与边长$\sqrt{2}$为的正方形CEFG如图摆放,连BG、DE.将正方形CEFG绕点C逆时针旋转.
将边长为$\sqrt{5}$的正方形ABCD与边长$\sqrt{2}$为的正方形CEFG如图摆放,连BG、DE.将正方形CEFG绕点C逆时针旋转.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com