练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．已知一次函数y=2x+4
    （1）在如图所示的平面直角坐标系中，画出函数的图象；
    （2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；
    （3）在（2）的条件下，求出△AOB的面积；
    （4）利用图象直接写出：当y＜0时，x的取值范围．

    分析 （1）利用两点法就可以画出函数图象；（2）利用函数解析式分别代入x=0与y=0的情况就可以求出交点坐标；（3）通过交点坐标就能求出面积；（4）观察函数图象与x轴的交点就可以得出结论．

    解答 解：（1）当x=0时y=4，当y=0时，x=-2，则图象如图所示

    （2）由上题可知A（-2，0）B（0，4），
    （3）S△AOB=$\frac{1}{2}$×2×4=4，
    （4）x＜-2．

    点评 本题考查了一次函数的图象和一次函数图象上点的坐标特征．正确求出一次函数与x轴与y轴的交点是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

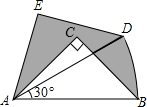    1．如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为BD，则图中阴影部分的面积是（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{2}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知反比例函数y=$\frac{k}{x}$的图象经过点（2，-1），则k=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

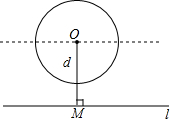    19．如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m=4，由此可知：
    （1）当d=3时，m=1；
    （2）当m=2时，d的取值范围是1＜d＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

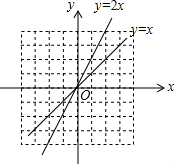    6．如图，把函数y=x的图象上各点的纵坐标变为原来的2倍，横坐标不变，得到函数y=2x的图象；也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变，得到函数y=2x的图象．
    类似地，我们可以认识其他函数．
    （1）把函数y=$\frac{1}{x}$的图象上各点的纵坐标变为原来的6倍，横坐标不变，得到函数y=$\frac{6}{x}$的图象；也可以把函数y=$\frac{1}{x}$的图象上各点的横坐标变为原来的6倍，纵坐标不变，得到函数y=$\frac{6}{x}$的图象．
    （2）已知下列变化：①向下平移2个单位长度；②向右平移1个单位长度；③向右平移$\frac{1}{2}$个单位长度；④纵坐标变为原来的4倍，横坐标不变；⑤横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变；⑥横坐标变为原来的2倍，纵坐标不变．
    （Ⅰ）函数y=x2的图象上所有的点经过④→②→①，得到函数y=4（x-1）2-2的图象；
    （Ⅱ）为了得到函数y=-$\frac{1}{4}$（x-1）2-2的图象，可以把函数y=-x2的图象上所有的点D．
    A．①→⑤→③B．①→⑥→③C．①→②→⑥D．①→③→⑥
    （3）函数y=$\frac{1}{x}$的图象可以经过怎样的变化得到函数y=-$\frac{2x+1}{2x+4}$的图象？（写出一种即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，正方形ABCD中，以对角线AC为一边作菱形AEFC，则∠FAB=22.5°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列结论错误的是（　　）
    A．对角线相等的菱形是正方形
    B．对角线互相垂直的矩形是正方形
    C．对角线互相垂直且相等的四边形是正方形
    D．对角线互相垂直且相等的平行四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．阅读下面材料：
    在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
    小敏在思考问题是，有如下思路：连接AC．

    结合小敏的思路作答
    （1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决以下问题：
    （2）如图2，在（1）的条件下，若连接AC，BD．
    ①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
    ②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

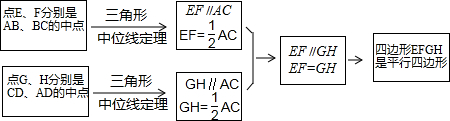
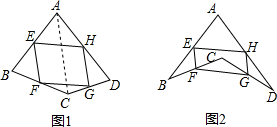
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

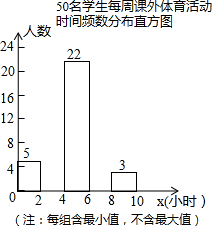    1．为增强学生体质，各学校普遍开展了阳光体育活动，某校为了解全校1000名学生每周课外体育活动时间的情况，随机调查了其中的50名学生，对这50名学生每周课外体育活动时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤x＜8小时的学生人数占24%．根据以上信息及统计图解答下列问题：
    （1）本次调查属于抽样调查，样本容量是50；
    （2）请补全频数分布直方图中空缺的部分；
    （3）求这50名学生每周课外体育活动时间的平均数；
    （4）估计全校学生每周课外体育活动时间不少于6小时的人数．

    查看答案和解析>>

    同步练习册答案