
已知关于x的方程mx2+(3m+1)x+3=0(m≠0).
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值;
(3)在(2)的条件下,将关于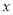 的二次函数y= mx2+(3m+1)x+3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请结合这个新的图象回答:当直线y=x+b与此图象有两个公共点时,b的取值范围.
的二次函数y= mx2+(3m+1)x+3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请结合这个新的图象回答:当直线y=x+b与此图象有两个公共点时,b的取值范围.
(1)证明略;(2)m=1;(3)1<b<3,b>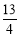 .
.
【解析】
试题分析:(1)求出根的判别式总是非负数即可;
(2)由求根公式求出两个解,令这两个解是整数求出m即可;
(3)先求出A、B的坐标,再根据图像得到b的取值范围.
试题解析:(1)证明:∵m≠0,∴mx2+(3m+1)x+3=0是关于x的一元二次方程.
∴△=(3m+1)2-12m =(3m-1)2. ∵ (3m-1)2≥0, ∴方程总有两个实数根.
(2)【解析】
由求根公式,得x1=-3,x2=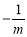 .
.
∵方程的两个根都是整数,且m为正整数, ∴m=1.
(3)【解析】
∵m=1时,∴y=x2+4x+3.
∴抛物线y=x2+4x+3与x轴的交点为A(-3,0)、B(-1,0).
依题意翻折后的图象如图所示.

当直线y=x+b经过A点时,可得b=3. 当直线y=x+b经过B点时,可得b=1. ∴1<b<3.
当直线y=x+b与y=-x2-4x-3 的图象有唯一公共点时,可得x+b=-x2-4x-3,
∴x2+5x+3+b=0, ∴△=52-4(3+b) =0,∴b=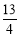 .∴b>
.∴b>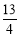 .
.
综上所述,b的取值范围是1<b<3,b>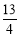 .
.
考点:根的判别式,求根公式的应用,函数的图像.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源:2014-2015学年福建省福鼎市十校教研联合体九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′ 处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
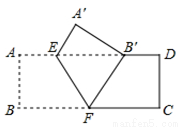
A.12 B.24 C. 12 D.16
D.16
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福鼎市十校教研联合体九年级上学期期中联考数学试卷(解析版) 题型:选择题
矩形具有而菱形不具有的性质是( )
A.对角线平分 B.对角线相等 C.对角线垂直 D.对角线平分对角
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市门头沟区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,一次函数y=kx+2的图象与x轴交于点B,与反比例函数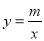 的图象的一个交点为(2,3).
的图象的一个交点为(2,3).

(1)分别求反比例函数和一次函数的表达式;
(2)过点A作AC⊥x轴,垂足为C,若点P在反比例函数图象上,且△PBC的面积等于18,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市门头沟区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)的对称轴是直线 ,
,
在下列结论中,唯一正确的是 .(请将正确的序号填在横线上)

① a<0;② c<-1; ③ 2a+3b=0;④ b2-4ac<0;⑤ 当x= 时,y的最大值为
时,y的最大值为 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市怀柔区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°, ,AD=4.
,AD=4.
求DC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com