
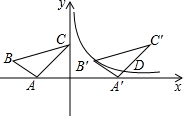
 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.分析 (1)根据平移的规律得到B'(2,2),再根据点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,即可得到k的值;
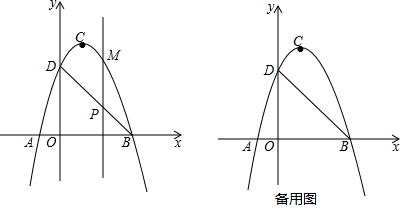
(2)根据|PB'-PD|≤B'D,可得当B'、D、P在同一直线上时,PB'-PD=B'D成立,此时线段PB′与线段PD之差最大,再设直线B'P解析式为y=ax+b,将D(5,$\frac{4}{5}$),B'(2,2)代入,可得直线B'P解析式,进而得出点P的坐标.
解答 解:(1)∵顶点B的坐标为(-5,2),将△ABC沿x轴向右平移7个单位得到△A′B′C′,
∴B'(2,2),
∵点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,
∴k=2×2=4,
∴反比例函数的表达式为y=$\frac{4}{x}$;
(2)如图所示,连接PB',PD,B'D,
∵|PB'-PD|≤B'D,
∴当B'、D、P在同一直线上时,PB'-PD=B'D成立,
此时线段PB′与线段PD之差最大,
设直线B'P解析式为y=ax+b,
把D(5,$\frac{4}{5}$),B'(2,2)代入,可得
$\left\{\begin{array}{l}{\frac{4}{5}=5a+b}\\{2=2a+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{2}{5}}\\{b=\frac{14}{5}}\end{array}\right.$,
∴直线B'P解析式为y=-$\frac{2}{5}$x+$\frac{14}{5}$,
令y=0,则0=-$\frac{2}{5}$x+$\frac{14}{5}$,
解得x=7,
∴P(7,0).
点评 本题主要考查了待定系数法求反比例函数解析式以及坐标与图形变化的运用,解题时注意:把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度.


科目:初中数学 来源: 题型:解答题
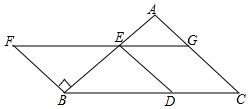 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
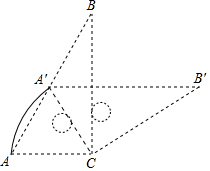 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )| A. | πcm | B. | 2πcm | C. | $\frac{8π}{3}cm$ | D. | 4πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
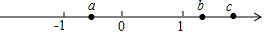 已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|
已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|查看答案和解析>>
科目:初中数学 来源: 题型:填空题
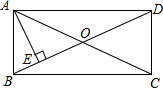 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com