
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
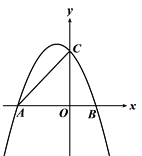
【答案】(1) A(﹣4,0),B(2,0);(2)△ACP最大面积是4.
【解析】
(1)令y=0,得到关于x 的一元二次方程﹣![]() x2﹣x+4=0,解此方程即可求得结果;
x2﹣x+4=0,解此方程即可求得结果;
(2)先求出直线AC解析式,再作PD⊥AO交AC于D,设P(t,﹣![]() t2﹣t+4),可表示出D点坐标,于是线段PD可用含t的代数式表示,所以S△ACP=
t2﹣t+4),可表示出D点坐标,于是线段PD可用含t的代数式表示,所以S△ACP=![]() PD×OA=
PD×OA=![]() PD×4=2PD,可得S△ACP关于t 的函数关系式,继而可求出△ACP面积的最大值.
PD×4=2PD,可得S△ACP关于t 的函数关系式,继而可求出△ACP面积的最大值.
(1)解:设y=0,则0=﹣![]() x2﹣x+4
x2﹣x+4
∴x1=﹣4,x2=2
∴A(﹣4,0),B(2,0)
(2)作PD⊥AO交AC于D

设AC解析式y=kx+b
∴![]()
解得:![]()
∴AC解析式为y=x+4.
设P(t,﹣![]() t2﹣t+4)则D(t,t+4)
t2﹣t+4)则D(t,t+4)
∴PD=(﹣![]() t2﹣t+4)﹣(t+4)=﹣
t2﹣t+4)﹣(t+4)=﹣![]() t2﹣2t=﹣
t2﹣2t=﹣![]() (t+2)2+2
(t+2)2+2
∴S△ACP=![]() PD×4=﹣(t+2)2+4
PD×4=﹣(t+2)2+4
∴当t=﹣2时,△ACP最大面积4.


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )

A. 2 B. 2或6 C. 4或6 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
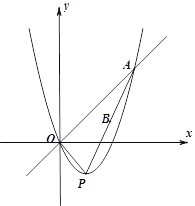
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠长为18m的墙,另三边用木栏围城,木栏长为32m.

(1)鸡场的面积能围成120m2吗?
(2)鸡场的面积能围成130m2吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习反比例函数的图象时,他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤,在纸上逐步探索函数y2=![]() 的图象,并且在黑板上写出4个点的坐标:A(
的图象,并且在黑板上写出4个点的坐标:A(![]() ,
,![]() ),B(1,2),C(1,
),B(1,2),C(1,![]() ),D(﹣2,﹣1).
),D(﹣2,﹣1).
(1)在A、B、C、D四个点中,任取一个点,这个点既在直线y1=x+1又在双曲线y2=![]() 上的概率是多少?
上的概率是多少?
(2)小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线y2=![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com