
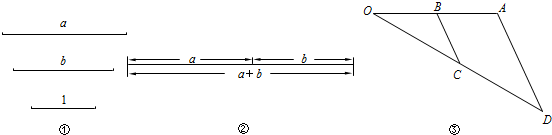
���� ���ӡ����������߶κͲ�弴�ɻ���ͼ��
���ˡ�����ƽ���߷��߶γɱ������������ɽ�����⣮
����������ƽ���߷��߶γɱ������������ɽ�����⣮
���������������������Σ����ɽ�����⣮
��� �⣺���ӡ�������ͼ�٣��߶�AB��Ϊa-b��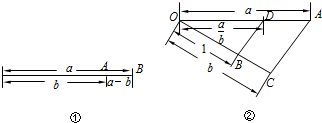
���ˡ�֤������AD��BC��
��$\frac{OB}{OA}$=$\frac{OC}{OD}$����$\frac{1}{a}$=$\frac{b}{OD}$��
��OD=ab��
��������ͼ�ڣ�OA=a��OC=b����B��OC�ϣ�OB=1��BD��AC����OA�ڵ�D��
��OD=$\frac{a}{b}$��
֤������BD��AC��
��$\frac{OD}{OA}$=$\frac{OB}{OC}$��
��$\frac{OD}{a}$=$\frac{1}{b}$��
��OD=$\frac{a}{b}$��
��������ͼ�ۺ�ͼ���е�MN��Ϊ$\sqrt{a+b}$��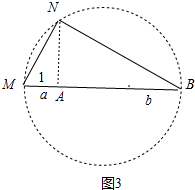
���ɣ���ͼ3�У�BM��ֱ����BM=a+b��AM=1��AN��BM��
�ߡ�M=��M����MAN=��MNB=90�㣬
���MAN�ס�MNB��
��$\frac{MN}{MA}$=$\frac{BM}{MN}$��
��MN2=a+b��
��MN=$\sqrt{a+b}$��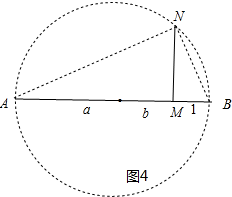
��ͼ4�У�AB��ֱ����AB=a+b+1��
BM=1��MN��AB��
�ɡ�AMN�ס�NMB��
��$\frac{MN}{BM}$=$\frac{AM}{MN}$��
��MN2=a+b��
��MN=$\sqrt{a+b}$��
���� ���⿼����ͼ-���Ӧ�á�ƽ���߷��߶γɱ������������������ε��ж������ʵ�֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3+x3=2x3 | B�� | x6��x2=x3 | C�� | x3•x2=x6 | D�� | ��x2��3=x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB�ǡ�O��ֱ����CD�ǡ�O���ң�����BAC=22�㣬���ADC�Ķ����ǣ�������
��ͼ��AB�ǡ�O��ֱ����CD�ǡ�O���ң�����BAC=22�㣬���ADC�Ķ����ǣ�������| A�� | 22�� | B�� | 58�� | C�� | 68�� | D�� | 78�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | -9 | C�� | 8 | D�� | -23 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ��ֱ������ϵ�У�����30������dzߵĶ���C���ڵڶ����ޣ���б�����˵�A��B�ֱ�����x�ᡢԭ���ϣ���AB=12cm��
��ͼ��ƽ��ֱ������ϵ�У�����30������dzߵĶ���C���ڵڶ����ޣ���б�����˵�A��B�ֱ�����x�ᡢԭ���ϣ���AB=12cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�ı���ABCD�У�BD��ACΪ�Խ��ߣ���������һ���ʵ���������2=��6���3=��7��ʹ��AB��CD������
��ͼ�ı���ABCD�У�BD��ACΪ�Խ��ߣ���������һ���ʵ���������2=��6���3=��7��ʹ��AB��CD�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com