
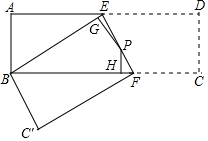
 如图,长方形ABCD中,AB=3cm,AD=9cm,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的一点,PG⊥BE,PH⊥BF,则PG+PH=4.
如图,长方形ABCD中,AB=3cm,AD=9cm,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的一点,PG⊥BE,PH⊥BF,则PG+PH=4. 分析 过点E作EQ⊥BF,垂足为Q,过点E作EQ⊥BC,垂足为Q,连接DF,如图,由矩形的性质得到AD=BC=9cm,CD=AB=3cm,∠C=∠ADC=90°.根据勾股定理得到CF=4,得到BF=BC-CF=AD-CF=5,根据矩形的性质得到EQ=DC=4.推出BE=BF,连接PB,根据三角形的面积公式即可得到结论.
解答 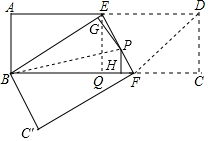 解:过点E作EQ⊥BC,垂足为Q,连接DF,如图,
解:过点E作EQ⊥BC,垂足为Q,连接DF,如图,
∵四边形ABCD是矩形,
∴AD=BC=9cm,CD=AB=3cm,∠C=∠ADC=90°.
由折叠可得:DF=BF,∠BEF=∠DEF.
∵∠C=90°,∴DC2+CF2=DF2,
∴32+CF2=(9-CF)2,
∴CF=4,
∴BF=BC-CF=AD-CF=5,
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC.
∴四边形EQCD是矩形,
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB.
∴BE=BF,
连接PB,
∴S△BEF=S△BEP+S△BPF,
即$\frac{1}{2}$BF•EQ=$\frac{1}{2}$BE•PG+$\frac{1}{2}$BF•PH=$\frac{1}{2}$BF•PG+$\frac{1}{2}$BF•PH,
∴PH+PG=EQ,
∴PG+PH=4.
即PG+PH的值为4.
故答案为:4.
点评 本题考查了矩形的性质与判定、等腰三角形的性质与判定、三角形的面积的计算,勾股定理等知识,正确的作出辅助线是解题的关键.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
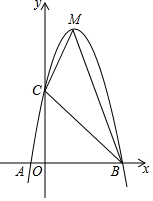 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
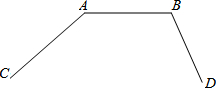 如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).
如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com