
【题目】如图,四边形 ABCD 为矩形,点 E 为 BC 上的一点,满足 AB CF BE CE ,连接 DE ,延长 EF交 AD 于 M 点,若 AE ![]() FD
FD ![]() AF
AF ![]() , DEF 15°,则M 的度数为_____.
, DEF 15°,则M 的度数为_____.
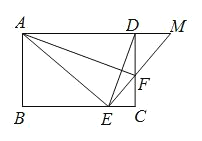
【答案】60°
【解析】
根据矩形的性质可得∠B=∠C=90°,AD∥BC,然后根据相似三角形的判定定理即可证出△ABE∽△ECF,从而得出∠AEB=∠EFC,然后求出∠AEF,结合勾股定理和已知条件即可证出EF=FD,根据等边对等角可得∠DEF=∠EDF=15°,然后根据三角形外角的性质、平行线的性质即可求出结论.
解:∵四边形 ABCD 为矩形,
∴∠B=∠C=90°,AD∥BC
∴∠EFC+∠FEC=90°
∵AB CF BE CE ,
∴![]()
∴△ABE∽△ECF
∴∠AEB=∠EFC
∴∠AEB+∠FEC=90°
∴∠AEF=180°-(∠AEB+∠FEC)=90°
在Rt△AEF中,AE![]() EF
EF![]() AF
AF![]() ,
,
∵AE![]() FD
FD![]() AF
AF![]() ,
,
∴EF=FD
∴∠DEF=∠EDF=15°
∴∠EFC=∠DEF+∠EDF=30°
∴∠FEC=90°-∠EFC=60°
∵AD∥BC
∴∠M=∠FEC=60°
故答案为:60°.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE为等腰直角三角形,∠BAC=∠DEC=90°,连接AD,取AD中点P,连接BP,并延长到点M,使BP=PM,连接AM、EM、AE,将△CDE绕点C顺时针旋转.
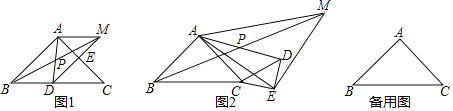
(1)如图①,当点D在BC上,E在AC上时,AE与AM的数量关系是______,∠MAE=______;
(2)将△CDE绕点C顺时针旋转到如图②所示的位置,(1)中的结论是否仍然成立,若成立,请给出证明,若不成立,请说明理由;
(3)若CD=![]() BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=
BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=![]() CD时,请直接写出α的值.
CD时,请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒 肺炎的防护知识,并鼓励社区居民在线参与作答《2020 年新型冠状病毒防治全国统一考试 (全国卷)》试卷(满分 100 分),社区管理员随机从甲、乙两个小区各抽取 20 名人员的 答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 | |
甲小区 | 2 | 5 | 8 | 5 |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
平均数 | 中位数 | 众数 | |
甲小区 | 85.75 | 87.5 | a |
乙小区 | 83.5 | b | 80 |
应用数据
(1)填空:a = ,b =___,
(2)若甲小区共有 800 人参与答卷,请估计甲小区成绩大于 90 分的人数为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.

(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的两个动点(与点
上的两个动点(与点![]() 、
、![]() 、
、![]() 不重合),且始终保持
不重合),且始终保持![]() ,
,![]() ,
,![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
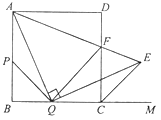
(1)求证:![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,并求出此时
,并求出此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 为正方形,取 AB 中点O ,以 AB 为直径, O 圆心作圆.
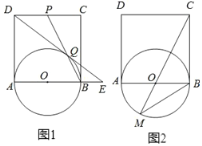
(1)如图 1,取CD 的中点 P ,连接 BP 交⊙ O 于Q ,连接 DQ 并延长交 AB 的延长线于 E ,求证: QE ![]() BE AE ;
BE AE ;
(2)如图 2,连接 CO 并延长交⊙ O 于 M 点,求tanM 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】名闻遐迩的采花毛尖明前茶,成本每厅400元,某茶场今年春天试营销,每周的销售量y(斤)是销售单价x(元/斤)的一次函数,且满足如下关系:
x(元/斤) | 450 | 500 | 600 |
y(斤) | 350 | 300 | 200 |
(1)请根据表中的数据求出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利不少于30000元,试确定销售单价x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
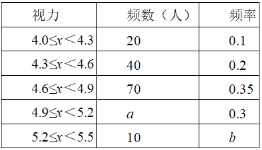
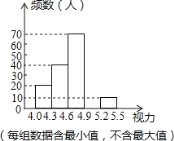
(1)本次调查的样本为 ,样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
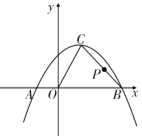
【题目】已知:如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)试确定该抛物线的函数表达式;
(2)已知点![]() 是该抛物线的顶点,求
是该抛物线的顶点,求![]() 的面积;
的面积;
(3)若点![]() 是线段
是线段![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com