
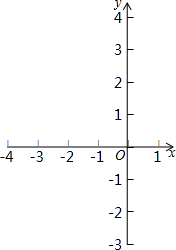 ��֪����x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0����������ȵ�ʵ������kΪ��������
��֪����x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0����������ȵ�ʵ������kΪ������������ ��1���ȸ���һԪ���η��̸�����������б�ʽ��0�Ĺ�ϵ�������k��ֵ��
��2������m�ȱ�ʾ��M��N�����꣬�ٸ��������ľ��빫ʽ��ʾ��MN�ij��ȣ����ݶ��κ����ļ�ֵ�������MN����Ⱥ�M�����ꣻ
��3������ͼ����ص㣬������������ۣ��ֱ����b��ֵ���ɣ�
��� �⣺��1���߹���x��һԪ���η���${x}^{2}+2x+\frac{k-1}{2}=0$����������ȵ�ʵ������
��$��={b}^{2}-4ac=4-4��\frac{k-1}{2}��0$��
��k-1��2��
��k��3��
��k��������
��kΪ1��2��
��2����x=0���뷽��${x}^{2}+2x+\frac{k-1}{2}=0$��k=1��
��ʱ���κ���Ϊy=x2+2x��
��ʱֱ��y=x+2����κ���y=x2+2x�Ľ���ΪA��-2��0����B��1��3��
���������M��m��m+2��������-2��m��1��
��N��m��m2+2m����
MN=m+2-��m2+2m��=-m2-m+2=-$��m+\frac{1}{2}��^{2}+\frac{9}{4}$��
�൱m=-$\frac{1}{2}$ʱ��MN�ij������ֵΪ$\frac{9}{4}$��
��ʱ��M������Ϊ$��-\frac{1}{2}��\frac{3}{2}��$��
��3����y=$\frac{1}{2}$x+b����Aʱ��ֱ������ͼ����3�������㣨��ͼ2��ʾ����
��A��-2��0������y=$\frac{1}{2}$x+b��b=1��
��y=$\frac{1}{2}$x+b����ͼ��ķ�ղ�����һ��������ʱ��ֱ������ͼ����3�������㣮
������ͼ��ķ�ղ�����ԭͼ��ķ�ղ��ֹ���x��Գƣ����������ʽΪy=-x2-2x
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-{x}^{2}-2x}\end{array}\right.$��һ��⣬��ʱ$-{x}^{2}-\frac{5}{2}x-b=0$��������ȵ�ʵ������
��$��\frac{5}{2}��^{2}-4b=0$����b=$\frac{25}{16}$��
��������b=1��b=$\frac{25}{16}$��
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˸����б�ʽ��Ӧ�ã���������������ͼ��Ľ������⣬�ѵ����ڣ�3�����ֱ������������3��������������������������ۣ���������ͼ�θ����ڽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| Ь�ij��루��λ��cm�� | 23 | 23.5 | 24 | 24.5 | 25 |
| ����������λ��˫�� | 1 | 2 | 2 | 5 | 1 |
| A�� | 23.5��24 | B�� | 24��24.5 | C�� | 24��24 | D�� | 24.5��24.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+x4=x6 | B�� | x6��x3=x2 | ||
| C�� | $\frac{-a-b}{a+b}$=-1 | D�� | $\frac{b}{{a}^{2}-{b}^{2}}$�£�1-$\frac{a}{a+b}$��=-$\frac{1}{a-b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���C=90�㣬BD�ǡ�ABC��һ����ƽ���ߣ���O��E��F�ֱ���BD��BC��AC�ϣ����ı���OECF�������Σ�
��ͼ����Rt��ABC�У���C=90�㣬BD�ǡ�ABC��һ����ƽ���ߣ���O��E��F�ֱ���BD��BC��AC�ϣ����ı���OECF�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
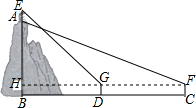 ѧϰ���������Ǻ�����ߡ���ij�ۺ�ʵ���С��ʵ�ز����˷��ɽ�����Ĺ㳡����Ը߶�AB��������������£�
ѧϰ���������Ǻ�����ߡ���ij�ۺ�ʵ���С��ʵ�ز����˷��ɽ�����Ĺ㳡����Ը߶�AB��������������£��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com