
在Rt△ABC中,∠ACB=90°,BC=30,AB=50,点P是AB边上任意一点,直线PE⊥AB,与边AC相交于E,此时Rt△AEP∽Rt△ABC,点M在线段AP上,点N在线段BP上,EM=EN,EP:EM=12:13.
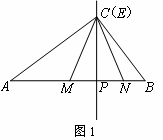
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A,C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围.

(1)CM=26;(2)y=50-![]() x,0<x<32
x,0<x<32
【解析】
试题分析:(1)先根据已知条件得出AC的值,再根据CP⊥AB求出CP,从而得出CM的值;
(2)先根据sin∠EMP=![]() ,设出EP的值,从而得出EM和PM的值,再得出△AEP∽△ABC,即可求出
,设出EP的值,从而得出EM和PM的值,再得出△AEP∽△ABC,即可求出![]() ,求出a的值,即可得出y关于x的函数关系式,并且能求出x的取值范围.
,求出a的值,即可得出y关于x的函数关系式,并且能求出x的取值范围.
解: (1)∵∠ACB=90°,
∴![]()
![]() ,
,
∵CP⊥AB,
∴![]()
∴![]() ,
,
∴CP=24,
∴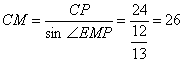 ;
;
(2)∵sin∠EMP=![]() ,
,
∴设EP=12a,则EM=13a,PM=5a,
∵EM=EN,
∴EN=13a,PN=5a,
∵△AEP∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴x=16a,
∴![]() ,
,
∴BP=50-16a,
∴y=50-21a=50-21×![]() =50-
=50-![]()
∵当E点与A点重合时,x=0.当E点与C点重合时,x![]() =32.
=32.
∴x的取值范围是:(0<x<32).


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com