练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，在锐角△ABC中，BA＝BC，点O是边AB上的一个动点(不与点A、B重合)，以O为圆心，OA为半径的圆交边AC于点M，过点M作⊙O的切线MN交BC于点N

    (1)当OA=OB时，求证：MN⊥BC；

    (2)分别判断OA＜OB、OA＞OB，上述结论是否成立?请选择一种情况说明理由．

    答案：略
    解析：

    (1)连接BM、OM，则，OM∥BC；

    (2)答OA＜OB时，成立：当OA＞OB时，也成立．

    如图所示，以OA＜OB为例证明如下：连接OM，

    ∵OA=OM，

    ∴∠A=∠OMA．

    ∵BA=BC，

    ∴∠A=∠C．∴OMA=∠C．OM∥BC．

    ∵MN为⊙O切线，

    ∴∠OMN=90°．∴∠MNC=∠OMN=90°．

    即MN⊥BC．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    7、如图所示，在锐角三角形ABC中，BD，CE分别是AC，AB边上的高，且BD，CE交于点F，若∠A=52°，则∠BFC的度数是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下面的材料，并回答所提出的问题：如图所示，在锐角三角形ABC中，求证：
    b
    sinB
    =
    c
    sinC

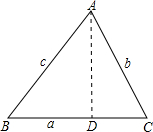    这个三角形不是一个直角三角形，不能直接使用锐角三角函数的知识去处理，所以必须构造直角三角形，精英家教网过点A作AD⊥BC，垂足为D，则在Rt△ABD和Rt△ACD中由正弦定义可完成证明．
    解：如图，过点A作AD⊥BC，垂足为D，
    在Rt△ABD中，sinB=
    AD
    AB
    ，则AD=csinB
    Rt△ACD中，sinC=
    AD
    AC
    ，则AD=bsinC
    所以c sinB=b sinC，即
    b
    sinB
    =
    c
    sinC

    （1）在上述分析证明过程中，主要用到了下列三种数学思想方法的哪一种（　　）
    A、数形结合的思想；B、转化的思想；C、分类的思想
    （2）用上述思想方法解答下面问题．
    在△ABC中，∠C=60°，AC=6，BC=8，求AB和△ABC的面积．
    （3）用上述结论解答下面的问题（不必添加辅助线）
    在锐角三角形ABC中，AC=10，AB=5
    		6
    ，∠C=60°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图所示，在锐角△ABC中，AB＜AC，AD⊥BC，交BC于点D，E，F，G分别是BC，CA，AB的中点，求证：四边形DEFG是等腰梯形．

    查看答案和解析>>

    科目：初中数学 来源：《29.1.3 用推理方法研究四边形》2010年同步练习（B卷）（解析版） 题型：解答题

    如图所示，在锐角△ABC中，AB＜AC，AD⊥BC，交BC于点D，E，F，G分别是BC，CA，AB的中点，求证：四边形DEFG是等腰梯形．

    查看答案和解析>>

    科目：初中数学 来源：2009年江苏省连云港市中考数学原创试卷大赛（1）（解析版） 题型：解答题

    阅读下面的材料，并回答所提出的问题：如图所示，在锐角三角形ABC中，求证：
    这个三角形不是一个直角三角形，不能直接使用锐角三角函数的知识去处理，所以必须构造直角三角形，过点A作AD⊥BC，垂足为D，则在Rt△ABD和Rt△ACD中由正弦定义可完成证明．
    解：如图，过点A作AD⊥BC，垂足为D，
    在Rt△ABD中，sinB=，则AD=csinB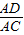
    Rt△ACD中，sinC=，则AD=bsinC
    所以c sinB=b sinC，即
    （1）在上述分析证明过程中，主要用到了下列三种数学思想方法的哪一种（ ）
    A、数形结合的思想；B、转化的思想；C、分类的思想
    （2）用上述思想方法解答下面问题．
    在△ABC中，∠C=60°，AC=6，BC=8，求AB和△ABC的面积．
    （3）用上述结论解答下面的问题（不必添加辅助线）
    在锐角三角形ABC中，AC=10，AB=，∠C=60°，求∠B的度数．

    查看答案和解析>>

    同步练习册答案