
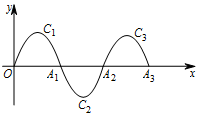
 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 不确定 |
分析 根据抛物线与x轴的交点问题,得到图象C1与x轴交点坐标为:(0,0),(2,0),再利用旋转的性质得到图象C2与x轴交点坐标为:(2,0),(4,0),则抛物线C2:y=(x-2)(x-4)(2≤x≤4),于是可推出横坐标x为偶数时,纵坐标为0,横坐标是奇数时,纵坐标为1或-1,只要判断n的值即可解决问题.
解答 解:∵一段抛物线C1:y=-x(x-2)(0≤x≤2),
∴图象C1与x轴交点坐标为:(0,0),(2,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;,
∴抛物线C2:y=(x-2)(x-4)(2≤x≤4),
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
∴P(2017,m)在抛物线C1009上,
∵n=1009是奇数,
∴P(2017,m)在x轴的上方,m=1,
∴当x=2017时,m=1.
故选C,
点评 本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
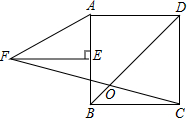 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )| A. | 60° | B. | 67.5° | C. | 75° | D. | 54° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-b=6 | B. | a+b=-10 | C. | a•b=-8 | D. | $\frac{a}{b}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
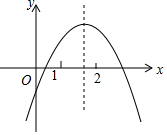 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0; ④a+b+c<0;⑤4a-2b+c>0,其中的正确结论是①③⑤(填写序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0; ④a+b+c<0;⑤4a-2b+c>0,其中的正确结论是①③⑤(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
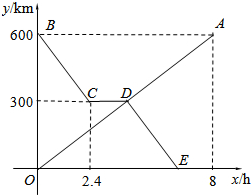 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
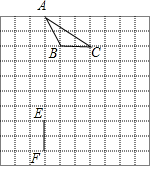 如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
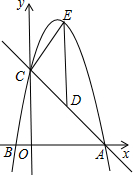 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com