练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如果将一个多边形的所有内角从小到大排列，恰好依次增加相同的度数，且最小内角的数是100°，最大内角的度数是140°，试求此多边形的边数．

    分析 设边数为n，增加相同度数为x，根据依次增加相同的度数，从100°增加到了140°，用n表示出x，再根据n边形的内角和进行列方程求解．

    解答 解：设边数为n，增加相同度数为x，
    则：100+（n-1）x=140，
    解得：x=$\frac{40}{n-1}$．
    又因为（n-2）•180=n•100+$\frac{n（n-1）}{2}$=n•100+n•20，
    解得：n=6．

    点评 此题主要考查了多边形内角与外角，用增加相同的度数x表示出多边形的内角和，即100+100+x+100+2x+…+100+（n-1）x=n•100+（1+2+…+n-1）x=100n+$\frac{n（n-1）}{2}$是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，b，c．
    （1）若b=2，c=3，求a的值；
    （2）若a：c=3：5，b=28，求a，c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

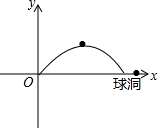    8．如图，老童在一次高尔夫球的练习中，在原点O处击球，球的飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x，其中y表示球飞行的高度（单位：米），x表示球飞行的水平距离（单位：米），结果球的落地点离球洞2米（击球点、落地点、球洞三点共线）．
    （1）求击球点O与球洞的距离；
    （2）当球的飞行高度不低于3米时，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．求下列各式的值：
    （1）1-2sin30°cos30°；
    （2）3tan30°-tan45°+2sin60°；
    （3）（cos230°+sin230°）×tan60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$相交于点A、B，与y轴交于点C，与x轴交于D，过点A作AE⊥x轴于点E，点O为DE中点，连接CE，已知S△ADE=4，tan∠DCO=$\frac{1}{2}$．
    （1）求y1和y2的解析式；
    （2）将△ACE绕着点E顺时针旋转90°得△A′C′E，连接AA′、BA′，求△AA′B的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．为了鼓励城区居民节约用水，某市规定用水收费标准如下：
     每户居民一个月用水量的范围 水费价格（范围：元/立方米）
     不超过20立方米 a
     超过20立方米不超过部分仍为a元，超过部分为b元
    已知某用户2014年十一月份用水15立方米，交水费22.5元，十二月份用水30立方米，交水费50元．
    （1）求a，b的值；
    （2）当用户居民月用水量为x立方米时，请用含x的式子表示应付水费；
    （3）若估计该用户2015年一月份的水费支出大概是65±1元，求该用户该月份的用水量x的可能整数值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．化简求值3a2-（5a2-ab+b2）-（7ab-7b2-3a2），其中a=-1，b=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．指出函数y=-2x2-8x-12的开口方向、对称轴、顶点坐标及最值并画出草图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）利用网格线作图1：在BC上找一点P，使点P到AB和AC的距离相等．然后在射线AP上找一点Q，使QB=QC．
    （2）如图2，在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD．
    （3）如图3，在直线l上找一点P，使得|PA-PB|的值最大．

    查看答案和解析>>

    同步练习册答案