
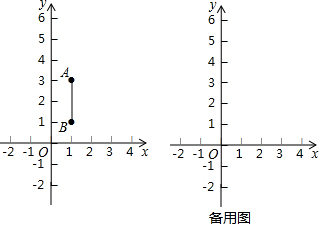
分析 (1)①根据“亲近点”的定义,观察图象可知,关于线段AB的“亲近点”是点P2,P3.②如图1中,题意AB∥A1B1,$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{1}{3}$,由AB=2,推出A1B1=6,由此即可解决问题.
(2)如图2中,设⊙C与y轴X相切于点G,过点O作⊙C的切线交AB于T,切点为F.首先证明OT⊥AB,当⊙E与OT相切时,且⊙E上的所有点都是关于⊙C的“亲近点”,此时EB=$\frac{5}{2}$,E($\frac{7}{4}$,$\frac{5\sqrt{3}}{4}$),当⊙E′与y轴相切时,且⊙E′上的所有点都是关于⊙C的“亲近点”,此时E(1,2$\sqrt{3}$),由此即可判断.
(3)如图,过点O作⊙M的切线OC、OD,切点为C、D.易知C($\frac{5}{3}$,$\frac{2\sqrt{5}}{3}$),D($\frac{5}{3}$,-$\frac{2\sqrt{5}}{3}$),由题意可知点Q、点T分别在线段OC、线段OD上时,⊙M上的所有点都是关于△NQT的“亲近点”,作点N关于直线OC的对称点N′,点N关于直线OC的对称点N″,连接N′N″,分别交OC、OD于Q、T,连接NQ,NT,此时△NTQ的周长最小,△NTQ的周长的最小值=QN+NT+QT=QN′+QT+TN″=N′N″.
解答 解:(1)①根据“亲近点”的定义,观察图象可知,关于线段AB的“亲近点”是点P2,P3.
故答案为P2,P3.
②如图1中,题意AB∥A1B1,$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{1}{3}$,
∵AB=2,
∴A1B1=6,
∴A1B1的最大值为6.
故答案为6.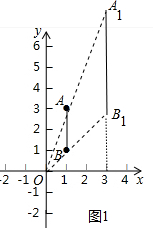
(2)如图2中,设⊙C与y轴X相切于点G,过点O作⊙C的切线交AB于T,切点为F.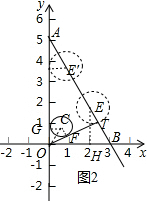
∵C($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
在Rt△COG和Rt∠COF中,tan∠COG=$\frac{CG}{OG}$=$\frac{\sqrt{3}}{3}$,
∴∠COG=∠COF=∠TOB=30°,
∵直线y=-$\sqrt{3}$x+3$\sqrt{3}$与x轴交于点B(3,0),与y轴交于点A(0,3$\sqrt{3}$),
∴tan∠BAO=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30°,
∴∠ABO=60°,
∴OT⊥AB,
∴OT=$\frac{OA•OB}{AB}$=$\frac{3\sqrt{3}}{2}$,TB=$\frac{3}{2}$,
当⊙E与OT相切时,且⊙E上的所有点都是关于⊙C的“亲近点”,此时EB=$\frac{5}{2}$,E($\frac{7}{4}$,$\frac{5\sqrt{3}}{4}$),
当⊙E′与y轴相切时,且⊙E′上的所有点都是关于⊙C的“亲近点”,此时E(1,2$\sqrt{3}$),
综上所述,满足条件的点E的纵坐标的取值范围为$\frac{5\sqrt{3}}{4}$≤yE≤2$\sqrt{3}$.
(3)如图,过点O作⊙M的切线OC、OD,切点为C、D.易知C($\frac{5}{3}$,$\frac{2\sqrt{5}}{3}$),D($\frac{5}{3}$,-$\frac{2\sqrt{5}}{3}$)
由题意可知点Q、点T分别在线段OC、线段OD上时,⊙M上的所有点都是关于△NQT的“亲近点”,
作点N关于直线OC的对称点N′,点N关于直线OC的对称点N″,连接N′N″,分别交OC、OD于Q、T,连接NQ,NT,此时△NTQ的周长最小,
易知N′($\frac{1}{9}$,$\frac{4\sqrt{5}}{9}$),N″($\frac{1}{9}$,-$\frac{4\sqrt{5}}{9}$),
∴△NTQ的周长的最小值=QN+NT+QT=QN′+QT+TN″=N′N″=$\frac{8\sqrt{5}}{9}$.
点评 本题考查圆综合题、一次函数的应用、直线与圆的位置关系,轴对称-最短问题、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用特殊位置解决问题,学会利用对称解决最短问题,属于中考压轴题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
 嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.
已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m≥1 | C. | m≥-1且m≠1 | D. | m>-1且m≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
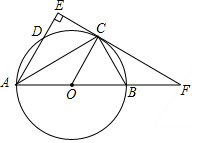 如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.
如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
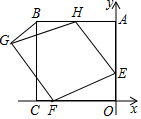 如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com