
分析 (1)根据总利润=单件利润×销售量列方程求解可得;
(2)根据(1)中相等关系列出函数解析式,再配方可得其最值情况.
解答 解:(1)设这种文具每件涨价x元时,销售利润为1920元,
根据题意,得:(30-20+x)(180-10x)=1920,
解得:x=2或x=8,
当x=2时,30+2=32<35,
当x=8时,30+8=38>35,舍去,
答:这种文具每件售价定为32元时,每个月销售利润恰好是1920元;
(2)设这种文具每件涨价x元时,每个月的利润为y元,
则y=(30-20+x)(180-10x)=-10(x-4)2+1960(0≤x≤5),
∴当x=4时,y最大值=1960,
答:这种文具每件售价定为34元时,可使每个月销售利润最大,最大的月利润是1960.
点评 本题考查了二次函数的应用,属于销售利润问题;要明确销售利润=每件的利润×销售的数量,解这类题的一般步骤是:①根据题意列出函数表达式,求出取值范围;②在自变量的取值范围内,运用公式法或配方法求出二次函数的最大值或最小值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
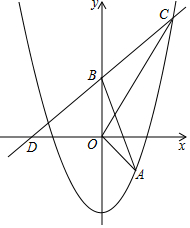 如图,在平面直角坐标系xOy中,抛物线y=ax2+c经过点A(1,-1),直线y=x+2与y轴交于点B、与抛物线在第一象限相交于点C,如果且∠BCO=∠OBA,求此抛物线的表达式.
如图,在平面直角坐标系xOy中,抛物线y=ax2+c经过点A(1,-1),直线y=x+2与y轴交于点B、与抛物线在第一象限相交于点C,如果且∠BCO=∠OBA,求此抛物线的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
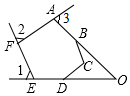 如图,六边形ABCDEF中,边AB、ED的延长线相交于O点,若图中三个外角∠1、∠2、∠3的和为230°,则∠BOD的度数为( )
如图,六边形ABCDEF中,边AB、ED的延长线相交于O点,若图中三个外角∠1、∠2、∠3的和为230°,则∠BOD的度数为( )| A. | 50° | B. | 60° | C. | 65° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
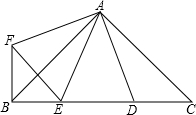 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
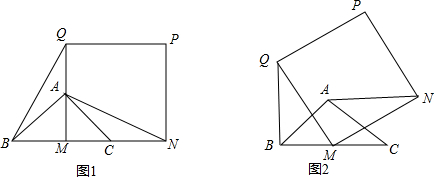
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com