
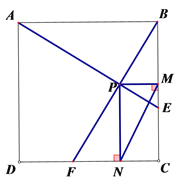
【题目】如图,四边形ABCD是边长为1的正方形,动点E、F分别从点C,D出发,以相同速度分别沿CB,DC运动(点E到达C时,两点同时停止运动).连接AE,BF交于点P,过点P分别作PM∥CD,PN∥BC,则线段MN的长度的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数![]() (天)与每天完成的工程量
(天)与每天完成的工程量![]() (
(![]() 天)的函数关系图象如图所示,是双曲线的一部分.
天)的函数关系图象如图所示,是双曲线的一部分.
![]() 请根据题意,求
请根据题意,求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
![]() 若该工程队有
若该工程队有![]() 台挖掘机,每台挖掘机每天能够开挖水渠
台挖掘机,每台挖掘机每天能够开挖水渠![]() 米,问该工程队需用多少天才能完成此项任务?
米,问该工程队需用多少天才能完成此项任务?
![]() 如果为了防汛工作的紧急需要,必须在一个月内(按
如果为了防汛工作的紧急需要,必须在一个月内(按![]() 天计算)完成任务,那么每天至少要完成多少米?
天计算)完成任务,那么每天至少要完成多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
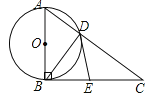
【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明:ED与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
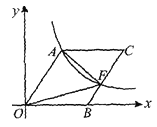
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
A. 10 B. 9 C. 8 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,CE AB于E, CD平分ECB, 交过点B的射线于D, 交AB于F, 且BC=BD.
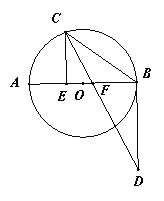
(1)求证:BD是⊙O的切线;
(2)若AE=9, CE=12, 求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F.

(1)求证:OE=OF;
(2)如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于![]() BD的所有的等腰三角形.
BD的所有的等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com