
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F. 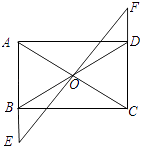
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴OB=OD(矩形的对角线互相平分),
AE∥CF(矩形的对边平行).
∴∠E=∠F,∠OBE=∠ODF.
∴△BOE≌△DOF(AAS)
(2)解:当EF⊥AC时,四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴OA=OC(矩形的对角线互相平分).
又∵由(1)△BOE≌△DOF得,OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)
又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形)
【解析】(1)由矩形的性质:OB=OD,AE∥CF证得△BOE≌△DOF;(2)若四边形EBFD是菱形,则对角线互相垂直,因而可添加条件:EF⊥AC,
当EF⊥AC时,∠EOA=∠FOC=90°,
∵AE∥FC,
∴∠EAO=∠FCO,矩形对角线的交点为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,根据对角线互相垂直平分的四边形是菱形.
∴四边形EBFD是菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法和矩形的性质的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A.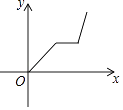
B.
C.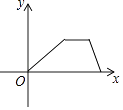
D.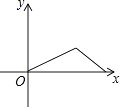
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由左边到右边的变形中,属于分解因式的是( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.10x2﹣5x=5x(2x﹣1)
D.x2﹣16+6x=(x+4)(x﹣4)+6x
查看答案和解析>>
科目:初中数学 来源: 题型:
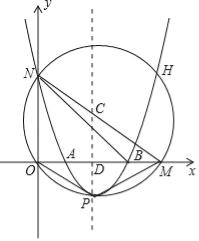
【题目】如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为( )
A.25×10﹣7
B.2.5×10﹣6
C.0.25×10﹣5
D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学著作《九章算术》在世界数学史上首次正式引入负数,如果收入100元记作+100元,那么﹣90元表示( )
A. 支出10元B. 收入10元C. 支出90元D. 收入90元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续正整数按如下个规律排列
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ……… | |
第一行 | 1 | 2 | 3 | 4 | ||
第二行 | 8 | 7 | 6 | 5 | ||
第三行 | 9 | 10 | 11 | 12 | ||
第四行 | 16 | 15 | 14 | 13 | ||
第五行 | 17 | 18 | 19 | 20 | ||
……… |
若正整数2019位于第a行、第b列,则a+b=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com