
【题目】如图,在六边形ABCDEF中,AF∥CD,A140,C165.
(1)求B的度数;
(2)当D °时,AB∥DE?为什么?
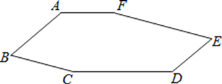
【答案】(1)°;(2)140°
【解析】
(1)过点B作BM∥AF,则BM∥AF∥CD,A140,C165,进而即可求解;
(2)延长AB,DC交于点N,由∠ABC=55°,CD165,得∠C=40°,结合AB∥DE,即可得到答案.
(1)过点B作BM∥AF,
∵AF∥CD,
∴BM∥AF∥CD,
∴∠A+∠ABM=180°,∠C+∠CBM=180°,
∵A140,C165,
∴B=∠ABM+∠CBM=360°-∠A-∠C=360°-140-165°.
(2)延长AB,DC交于点N,
∵∠ABC=55°,
∴∠NBC=125°,
∵CD165,
∴∠C165125°=40°
若AB∥DE,则∠D=180°-40°=140°.
故答案是:140°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,M、N分别是线段AC、BC的中点,
![]()
(1)若AC=7cm,BC=5cm,求线段MN的长;
(2)若AB=a,点C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;
(3)若将(2)中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
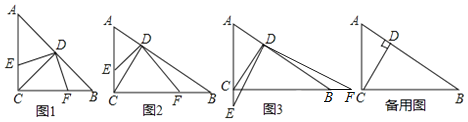
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
![]() 探究发现:
探究发现:
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym,图中的折线表示小亮在整个行走过程中y与x的函数关系.
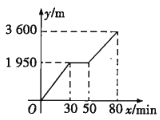
(1)小亮行走的总路程是________m;他途中休息了________min.
(2)①当![]() 时,求y与x的函数关系式.
时,求y与x的函数关系式.
②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
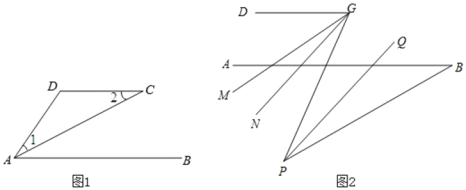
【题目】(1)如图1,AC平分DAB,12,试说明AB与CD的位置关系,并予以证明:
(2)如图2,在(1)的结论下,AB的下方点P满足ABP30,G是CD上任一点,PQ平分BPG,PQ∥GN,GM平分DGP,下列结论:
①DGPMGN的值不变;
②MGN的度数不变.
可以证明,只有一个是正确的,请你做出正确的选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
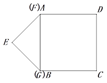
【题目】如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG
以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止
运动.设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大
致图象为( )
A. 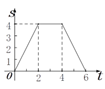 B.
B. 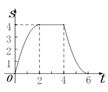 C.
C. 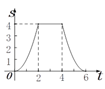 D.
D. 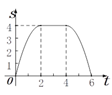
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com