
【题目】如图,在△ABC中,AB=AC,点D是边AB的点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
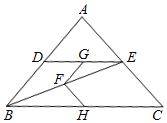
【答案】(1)见解析;(2)当∠A=90°时,FG⊥FH.
【解析】
(1)根据等腰三角形的性质得到∠ABC=∠ACB,根据平行线的性质、等腰三角形的判定定理得到AD=AE,得到DB=EC,根据三角形中位线定理证明结论;
(2)延长FG交AC于N,根据三角形中位线定理得到FH∥AC,FN∥AB,根据平行线的性质解答即可.
(1)证明:∵AB=AC.
∴∠ABC=∠ACB,∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=![]() BD,FH=
BD,FH=![]() CE,
CE,
∴FG=FH;
(2)解:延长FG交AC于N,
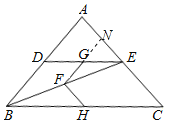
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
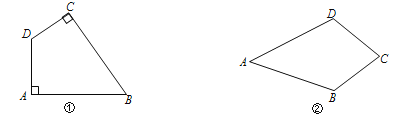
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
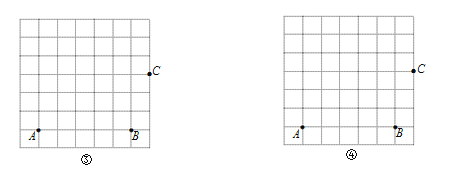
(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
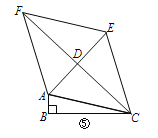
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与![]() 轴交于点C,顶点为D,对称轴与
轴交于点C,顶点为D,对称轴与![]() 轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交
轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交![]() 轴交于点G.
轴交于点G.
(1)如图①,求直线CE的解析式和顶点D的坐标;
(2)如图①,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于![]() 轴的直线l上一点,点N是抛物线对称轴上一点,求
轴的直线l上一点,点N是抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)如图②,过点D作![]() 交
交![]() 轴于点I,将△GDI沿射线GB方向平移至
轴于点I,将△GDI沿射线GB方向平移至![]() 处,将
处,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,当旋转到一定度数时,点
,当旋转到一定度数时,点![]() 会与点I重合,记旋转过程中的
会与点I重合,记旋转过程中的![]() 为
为![]() ,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )

A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com