
【题目】某班老师要求每人每学期读4~7本书,并随机抽查了本学期学生读课外书册数的情况,绘制成不完整的条形图和不完整的扇形图,其中条形图被墨迹遮盖了一部分,回答下列问题:
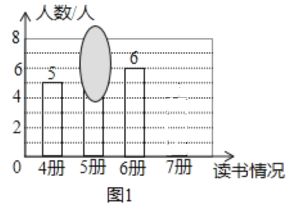

(1)请你求出老师随机抽查了多少名学生;
(2)已知册数的中位数是5,
嘉嘉说:条形图中被遮盖的数为5
淇淇说:条形图中被遮盖的数为6
ⅰ你认为嘉嘉和淇淇谁说的正确,请说明原因,并把条形图补充完整;
ⅱ在扇形图中,“7册”部分所对的圆心角为_______°,并把扇形图补充完整;
(3)请直接写出:从抽查学生中任取两人,恰好都读7册书的概率为_______.
【答案】(1)老师随机抽查了20名学生;(2)ⅰ淇淇说的正确,说明原因见解析;条型图见解析;ⅱ54,扇形图见解析;(3)![]() .
.
【解析】
(1)利用4册的频数和百分比即可得到总人数;
(2)i根据两个人的说法分别求中位数,若得到中位数是5即是正确,否则错误;
ⅱ用7册的数量除以总数20再乘以360°即可得到;
(3)20个人中设1、2、3每人读7册,每个人只能与另一个人被同时抽查,由此得到所有可能的情况,再列举同时抽查2个人的情况,即可利用概率公式计算得到答案.
(1)![]() 人,
人,
∴老师随机抽查了多少名学生;
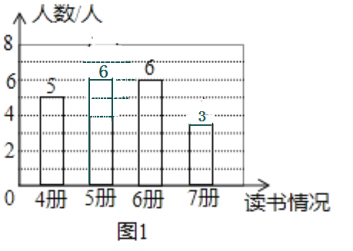
(2)ⅰ淇淇说的正确,
如果条形图中被遮盖的数为5,则册数的中位数是5.5,不符合题意;
如果条形图中被遮盖的数为6,则册数的中位数是5,
故淇淇说的正确;
7册的数量是:20-5-6-6=3(人),
条形图如下:
ⅱ“7册”部分的圆心角度数是![]() ,
,
故答案为:54

(3)20个人中设1、2、3每人读7册,
∵每个人只能与另一个人被同时抽查,
∴共有![]() 种可能的情况,
种可能的情况,
同时抽查2个人的情况有:(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)共6种,
∴从抽查学生中任取两人,恰好都读7册书的概率为![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
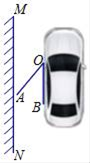
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成任务.
三角形的外心
定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心.
如图1,直线l1,l2,l3分别是边AB,BC,AC的垂直平分线.
求证:直线l1,l2,l3相交于一点.
证明:如图2,设l1,l2相交于点O,分别连接OA,OB,OC
∵l1是AB的垂直平分线,
∴OA=OB,(依据1)
∵l2是BC的垂直平分线,
∴OB=OC,
∴OA=OC,(依据2)
∵l3是AC的垂直平分线,
∴点O在l3上,(依据3)
∴直线l1,l2,l3相交于一点.
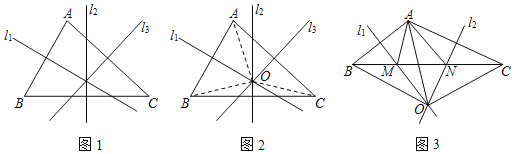
(1)上述证明过程中的“依据1”“依据2”“依据3”分别指什么?
(2)如图3,直线l1,l2分别是AB,AC的垂直平分线,直线l1,l2相交于点O,点O是△ABC的外心,l1交BC于点N,l2交BC于点N,分别连接AM、AN、OA、OB、OC.若OA=6cm,△OBC的周长为22cm,求△AMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=5,BC=8,点P在AB上,AP=1.将矩形ABCD沿CP折叠,点B落在点B'处.B'P、B′C分别与AD交于点E、F,则EF=_____.
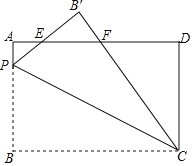
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】换个角度看问题.
(原题重现)
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
……
若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(问题再研)
若设慢车行驶的时间为x(h),慢车与甲地的距离为s1(km),第一列快车与甲地的距离为s2(km),第二列快车与甲地的距离为s3(km),根据原题中所给信息解决下列问题:
(1)在同一直角坐标系中,分别画出s1、s2与x之间的函数图象;
(2)求s3与x之间的函数表达式;
(3)求原题的答案.
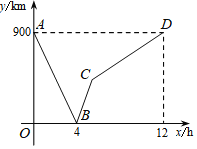
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() ,将扇形
,将扇形![]() 按图1摆放,使扇形的半径
按图1摆放,使扇形的半径![]() 、
、![]() 分别与
分别与![]() 、
、![]() 重合,
重合,![]() .
.
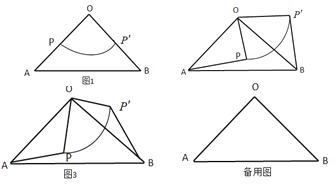
如图2,若![]() 不动,让扇形
不动,让扇形![]() 绕点
绕点![]() 逆时针旋转一周,连接线段
逆时针旋转一周,连接线段![]() 、
、![]() ,设旋转角为
,设旋转角为![]() .
.
发现:直接写出![]() 、
、![]() 的数量关系.
的数量关系.
探究:若![]()
(1)扇形![]() 绕到点
绕到点![]() 的左侧,当
的左侧,当![]() 时,旋转角
时,旋转角![]() ______°;
______°;
(2)扇形![]() 绕到点
绕到点![]() 的右侧,当
的右侧,当![]() 与
与![]() 相切时,求
相切时,求![]() ;
;
(3)若点![]() 是弧
是弧![]() 上任意一点,在扇形
上任意一点,在扇形![]() 绕点
绕点![]() 逆时针转过程中,当
逆时针转过程中,当![]() 的面积最大时,直接写出
的面积最大时,直接写出![]() 的度数;
的度数;
延伸:如图3,若![]() ,当
,当![]() 、
、![]() 、
、![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
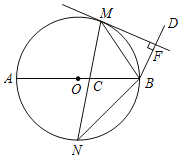
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com