
【题目】A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元.
(1)设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;

(2)求出总运费最低的调运方案,最低运费是多少?
【答案】(1)运费W关于x的函数关系式为W=20x+340 (4≤x≤10);
(2)运费最低是420元,运输方案是:从A校调运4台电脑到C校,调运8台电脑到D校,从B校调运6台电脑到C校.
【解析】(本题满分10分)
解:(1)由从A校调往C校x台可得:从A校调往D校(12-x)台,从B校调往C校(10-x)台,调往D校(6-(10-x))=(x-4)台
结合题意即可得到 W=40x+10(12-x)+30(10-x)+20(x-4)
所以,W=20x+340
因为机器的台数只能是正整数,所以
12x≥0且 10x≥0 且 x4≥0
解得:4≤x≤10,且x为正整数,
所以,运费W关于x的函数关系式为
W=20x+340 (4≤x≤10)
(2)结合一次函数的定义可知W=20x+340(4≤x≤10)是一次函数,
W随x的增大而增大,故当x=4时,运费W最低,此时W=420元
方案是:从A校调运4台电脑到C校,调运8台电脑到D校,从B校调运6台电脑到C校.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】用配方法解方程x2-8x+3=0,下列配方正确的是
A. (x-4)2=13 B. (x+4)2=13 C. (x-4)2=11 D. (x-4)2=-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。
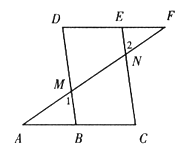
证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
课外体育锻炼情况扇形统计图
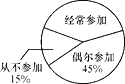
“经常参加”课外体育锻炼的男生最喜欢的一种项目条形统计图
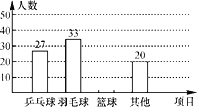
请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1 200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2,当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.
(1)t的取值范围为 ,AE cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
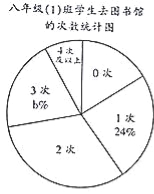
【题目】达州市图书馆今年4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图不完整的统计图表.
八年级(1)班学生去新图书馆的次数统计表
去图书馆的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 8 | 12 | a | 10 | 4 |
请你根据统计图表中的信息,解答下列问题:
(1)填空:a= ,b= ;
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受.求恰好抽中去过“4次及以上”的同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“感恩资助,立志成才”演讲比赛,根据初赛成绩在七,八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据图和下表提供的信息,解答下列问题:
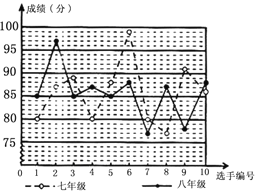
(1)请你把下边的表格填写完整;
成绩统计 | 众数 | 平均数 | 方差 |
七年级 | 85.7 | 39.61 | |
八年级 | 85.7 | 27.81 |
(2)考虑平均数与方差,你认为哪年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com