
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点. 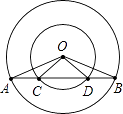
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
【答案】
(1)证明:∵OA=OB,OC=OD,
∴∠A=∠B,∠OCD=∠ODC,
∵∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,
∴∠A+∠AOC=∠BOD+∠B,
∴∠AOC=∠DOB
(2)解:AC=BD
证明:过O作OE⊥AB于E,
∴AE=EB,CE=ED,
∴AE﹣CE=BE﹣DE,
即AC=BD.

【解析】(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE﹣CE=BE﹣DE,即AC=BD.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠A=∠C;
B. AB∥CD,AD∥BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为8cm的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为xcm、ycm,剪去的两个小直角三角形的两直角边长也分别为xcm、ycm.

(1)用含有x、y的代数式表示图中“囧”(阴影部分)的面积.
(2)当x=8,y=2时,求此时“囧”(阴影部分)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 
A.a>0
B.当x≥1时,y随x的增大而增大
C.c<0
D.当﹣1<x<3时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点. 
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求![]() 的值.
的值.
(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则![]() =
=![]() =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则![]() =
=![]() =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以![]() 的值为2或﹣2.
的值为2或﹣2.
(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求![]() 的值;
的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现政府大力提倡绿色、低碳出行,越来越多的人选择用电动车出行,某商场销售的一款电动车每台的标价是3270元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款电动车每台的进价?(利润率=![]() =
=![]() ).
).
(2)在这次促销活动中,商场销售了这款电动车100台,问盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com