
°ĺŐ‚ńŅ°Ņ“—÷™ňńĪŖ–őABCDő™ĺō–ő£¨∂‘Ĺ«ŌŖAC°ĘBDŌŗĹĽ”ŕĶ„O£¨AD£ĹAO£ģĶ„E°ĘFő™ĺō–őĪŖ…ŌĶńŃĹłŲ∂ĮĶ„£¨«“°ŌEOF£Ĺ60°„£ģ
£®1£©»ÁÕľ1£¨ĶĪĶ„E°ĘF∑÷ĪūőĽ”ŕAB°ĘADĪŖ…Ō Ī£¨»Ű°ŌOEB£Ĺ75°„£¨«ů÷§£ļDF£ĹAE£Ľ
£®2£©»ÁÕľ2£¨ĶĪĶ„E°ĘFÕ¨ ĪőĽ”ŕABĪŖ…Ō Ī£¨»Ű°ŌOFB£Ĺ75°„£¨ ‘ňĶ√ųAF”ŽBEĶń żŃŅĻōŌĶ£Ľ
£®3£©»ÁÕľ3£¨ĶĪĶ„E°ĘFÕ¨ Ī‘ŕABĪŖ…Ō‘ň∂Į Ī£¨Ĺę°ųOEF—ōOEňý‘ŕ÷ĪŌŖ∑≠’Ř÷Ń°ųOEP£¨»°ŌŖ∂őCBĶń÷–Ķ„Q£ģѨŔPQ£¨»ŰAD£Ĺ2a£®a£ĺ0£©£¨‘ÚĶĪPQ◊Ó∂Ő Ī£¨«ůPF÷ģ≥§£ģ

°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©AF£Ĺ2BE£¨ľŻĹ‚őŲ£Ľ£®3£©![]() a
a
°ĺĹ‚őŲ°Ņ
£®1£©»ÁÕľ1÷–£¨‘ŕOD…Ō»°“ĽĶ„K£¨ ĻĶ√OK£ĹOE£¨Ń¨Ĺ”DK£ģŌŽįž∑®÷§√ųDK£ĹAE£¨DF£ĹDKľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®2£©»ÁÕľ2÷–£¨Ĺę°ųOAF»∆Ķ„Ońś Ī’Ž–ż◊™120°„Ķ√ĶĹ°ųOBJ£¨Ń¨Ĺ”JE£ģŌŽįž∑®÷§√ų°ŌJEB£Ĺ90°„£¨°ŌEJB£Ĺ30°„Ņ…Ķ√ĹŠ¬Ř£ģ
£®3£©»ÁÕľ3÷–£¨Ń¨Ĺ”BP£ģ÷§√ų°ųOAF°’°ųOBP£®SAS£©£¨Õ∆≥Ų°ŌPBC£Ĺ30°„£¨»ÁÕľ3©Ā1÷–£¨ĶĪQP°ÕPB Ī£¨PQĶń÷Ķ◊Ó–°£¨◊ųFH°ÕOA”ŕH£¨OM°ÕPF”ŕM£ģĹ‚÷ĪĹ«»żĹ«–ő«ů≥ŲFMľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®1£©÷§√ų£ļ»ÁÕľ1÷–£¨‘ŕOD…Ō»°“ĽĶ„K£¨ ĻĶ√OK£ĹOE£¨Ń¨Ĺ”DK£ģ
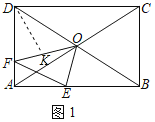
°ŖňńĪŖ–őABCD «ĺō–ő£¨
°ŗOD£ĹOA£¨°ŌDAB£Ĺ90°„£¨
°ŖAD£ĹAO£¨
°ŗAD£ĹAO£ĹOD£¨
°ŗ°ųOAD «Ķ»ĪŖ»żĹ«–ő£¨
°ŗ°ŌDOA£Ĺ°ŌEOF£Ĺ°ŌDAO£Ĺ°ŌADO£Ĺ60°„£¨
°ŗ°ŌDOK£Ĺ°ŌAOE£¨°ŌOAE£Ĺ90°„©Ā60°„£Ĺ30°„£¨
°ŖOD£ĹOA£¨OK£ĹOE£¨
°ŗ°ųDOK°’°ųAOE£®SAS£©£¨
°ŗDK£ĹAE£¨°ŌODK£Ĺ°ŌOAE£Ĺ30°„£¨
°ŖOA£ĹOB£¨
°ŗ°ŌOAB£Ĺ°ŌOBA£Ĺ30°„£¨
°Ŗ°ŌOEB£Ĺ75°„£¨
°ŗ°ŌOEB£Ĺ°ŌBOE£Ĺ75°„£¨
°Ŗ°ŌEOF£Ĺ60°„£¨
°ŗ°ŌDOK£Ĺ180°„©Ā75°„©Ā60°„£Ĺ45°„£¨
°ŗ°ŌDFO£Ĺ180°„©Ā60°„©Ā45°„£Ĺ75°„£¨°ŌDKO£Ĺ°ŌODK+°ŌDOK£Ĺ75°„£¨
°ŗ°ŌDFK£Ĺ°ŌDKF£Ĺ75°„£¨
°ŗDF£ĹDK£¨
°ŗDF£ĹAE£ģ
£®2£©Ĺ‚£ļĹŠ¬Ř£ļAF£Ĺ2BE£ģ
ņŪ”…£ļ»ÁÕľ2÷–£¨Ĺę°ųOAF»∆Ķ„Ońś Ī’Ž–ż◊™120°„Ķ√ĶĹ°ųOBJ£¨Ń¨Ĺ”JE£ģ

°Ŗ°ŌAOB£Ĺ120°„£¨°ŌEOF£Ĺ60°„£¨
°ŗ°ŌBOJ+°ŌBOE£Ĺ°ŌAOF+°ŌBOE£Ĺ60°„£¨
°ŗ°ŌEOJ£Ĺ°ŌEOF£¨
°ŖOF£ĹOJ£¨OE£ĹOE£¨
°ŗ°ųEOF°’°ųEOJ£®SAS£©£¨
°ŗ°ŌOEF£Ĺ°ŌOEJ£¨
°Ŗ°ŌOFB£Ĺ75°„£¨°ŌOBF£Ĺ30°„£¨
°ŗ°ŌBOF£Ĺ75°„£¨
°ŗ°ŌBOE£Ĺ75°„©Ā60°„£Ĺ15°„£¨
°ŗ°ŌFEO£Ĺ°ŌBOE+°ŌOBE£Ĺ45°„£¨
°ŗ°ŌOEF£Ĺ°ŌOEJ£Ĺ45°„£¨
°ŗ°ŌJEB£Ĺ°ŌJEF£Ĺ90°„£¨
°Ŗ°ŌOBJ£Ĺ°ŌOAF£Ĺ30°„£¨°ŌOBE£Ĺ30°„£¨
°ŗ°ŌEBJ£Ĺ60°„£¨
°ŗ°ŌEJB£Ĺ90°„©Ā60°„£Ĺ30°„£¨
°ŗBJ£Ĺ2BE£¨
°ŖAF£ĹBJ£¨
°ŗAF£Ĺ2BE£ģ
£®3£©Ĺ‚£ļ»ÁÕľ3÷–£¨Ń¨Ĺ”BP£ģ
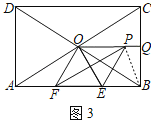
”…∑≠’ŘŅ…÷™£ļOE£ĹOP£¨°ŌEOF£Ĺ°ŌEOP£Ĺ60°„£¨
°ŗ°ŌFOP£Ĺ°ŌAOB£Ĺ120°„£¨
°ŗ°ŌAOF£Ĺ°ŌBOP£¨
°ŖOA£ĹOB£¨
°ŗ°ųOAF°’°ųOBP£®SAS£©£¨
°ŗ°ŌOBP£Ĺ°ŌOAF£Ĺ30°„£¨AF£ĹBP£¨
°Ŗ°ŌOBC£Ĺ60°„£¨
°ŗ°ŌPBC£Ĺ30°„£¨
»ÁÕľ3©Ā1÷–£¨ĶĪQP°ÕPB Ī£¨PQĶń÷Ķ◊Ó–°£¨◊ųFH°ÕOA”ŕH£¨OM°ÕPF”ŕM£ģ

‘ŕRt°ųPQB÷–£¨°Ŗ°ŌQPB£Ĺ90°„£¨°ŌPBQ£Ĺ30°„£¨BQ£Ĺ![]() BC£Ĺ
BC£Ĺ![]() AD£Ĺa£¨
AD£Ĺa£¨
°ŗPB£ĹAF£ĹBQcos30°„£Ĺ![]() a£¨
a£¨
‘ŕRt°ųAFH÷–£¨‘Ú”–AH£ĹAFcos30°„£Ĺ![]() a£¨FH£Ĺ
a£¨FH£Ĺ![]() AF£Ĺ
AF£Ĺ![]() £¨
£¨
°ŗOH£ĹOA©ĀAH£Ĺ2a©Ā![]() a£Ĺ
a£Ĺ![]() £¨
£¨
°ŗOF£Ĺ £¨
£¨
°ŖOF£ĹOP£¨OM°ÕPF£¨
°ŗFM£ĹMP£ĹOFcos30°„£Ĺ![]() £¨
£¨
°ŗFP£Ĺ2FM£Ĺ![]() a£ģ
a£ģ


 “ĽŌŖ√Ż ¶ŐŠ”Ň ‘ĺŪŌĶŃ–īūįł
“ĽŌŖ√Ż ¶ŐŠ”Ň ‘ĺŪŌĶŃ–īūįł —ŰĻ‚ ‘ĺŪĶ•‘™≤‚ ‘ĺŪŌĶŃ–īūįł
—ŰĻ‚ ‘ĺŪĶ•‘™≤‚ ‘ĺŪŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ňńĪŖ–őABCD÷–£¨BD «∂‘Ĺ«ŌŖ£¨![]() £¨
£¨![]() £¨
£¨![]() ĹĽDCĶń—”≥§ŌŖ”ŕE£¨»Ű
ĹĽDCĶń—”≥§ŌŖ”ŕE£¨»Ű![]() £¨
£¨![]() £¨‘ÚADĶń≥§ő™______£ģ
£¨‘ÚADĶń≥§ő™______£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
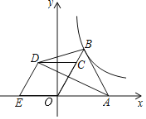
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ķ»ĪŖ°ųOABļÕŃ‚–őOCDEĶńĪŖOA£¨OE∂ľ‘ŕx÷Š…Ō£¨Ķ„C‘ŕOBĪŖ…Ō£¨S°ųABD£Ĺ![]() £¨∑īĪ»ņżļĮ ż
£¨∑īĪ»ņżļĮ ż![]() £®x£ĺ0£©ĶńÕľŌůĺ≠ĻżĶ„B£¨‘ÚkĶń÷Ķő™£® £©
£®x£ĺ0£©ĶńÕľŌůĺ≠ĻżĶ„B£¨‘ÚkĶń÷Ķő™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
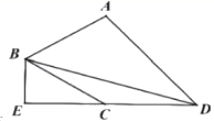
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ![]() ÷–£¨
÷–£¨![]() £¨Ķ„
£¨Ķ„![]() ő™
ő™![]() …Ō“ĽĶ„£¨“‘Ķ„
…Ō“ĽĶ„£¨“‘Ķ„![]() ő™‘≤–ń£¨
ő™‘≤–ń£¨![]() ő™įŽĺ∂Ķń
ő™įŽĺ∂Ķń![]() ”Ž
”Ž![]() Ōŗ«–”ŕĶ„
Ōŗ«–”ŕĶ„![]() £¨
£¨![]() ĹĽ
ĹĽ![]() Ķń—”≥§ŌŖ”ŕĶ„
Ķń—”≥§ŌŖ”ŕĶ„![]() £ģ
£ģ

£®1£©«ů÷§£ļ![]() £Ľ
£Ľ
£®2£©»Ű![]() £¨
£¨![]() £¨«ů
£¨«ů![]() ĶńįŽĺ∂ļÕ
ĶńįŽĺ∂ļÕ![]() Ķń≥§£ģ
Ķń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
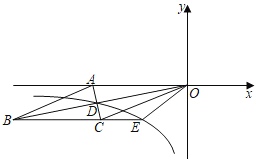
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ń‚–őOABCĶń“ĽĪŖOA‘ŕx÷ŠłļįŽ÷Š…Ō£ģO «◊ÝĪÍ‘≠Ķ„£¨Ķ„A(©Ā13£¨0)£¨∂‘Ĺ«ŌŖAC”ŽOBŌŗĹĽ”ŕĶ„D£¨«“ACOB£Ĺ130£¨»Ű∑īĪ»ņżļĮ ży£Ĺ![]() £®x£ľ0£©ĶńÕľŌůĺ≠ĻżĶ„D£¨≤Ę”ŽBCĶń—”≥§ŌŖĹĽ”ŕĶ„E£ģ
£®x£ľ0£©ĶńÕľŌůĺ≠ĻżĶ„D£¨≤Ę”ŽBCĶń—”≥§ŌŖĹĽ”ŕĶ„E£ģ
£®1£©«ůňę«ķŌŖy£Ĺ![]() ĶńĹ‚őŲ Ĺ£Ľ
ĶńĹ‚őŲ Ĺ£Ľ
£®2£©«ůS°ųAOB£ļS°ųOCE÷ģ÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
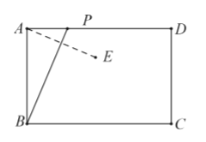
°ĺŐ‚ńŅ°Ņń≥–£Ņ™’Ļ’ųőńĽÓ∂Į£¨’ųőń÷ųŐ‚÷Ľń‹ī”°įįģĻķ°Ī°Ę°įĺī“Ķ°Ī°Ę°į≥Ō–Ň°Ī°Ę°į”—…∆°ĪňńłŲ÷ųŐ‚÷–—°‘Ů“ĽłŲ£¨√Ņ√Ż—ß…ķįī“™«ů∂ľ…ŌĹĽŃň“Ľ∑›’ųőń£¨—ß–£ő™ŃňĹ‚—°‘Ůłų÷÷’ųőń÷ųŐ‚Ķń—ß…ķ»ň ż£¨ňśĽķ≥ť»°Ńň≤Ņ∑÷’ųőńĹÝ––ŃňĶų≤ť£¨łýĺ›Ķų≤ťĹŠĻŻĽś÷∆≥…»ÁŌ¬ŃĹ∑ý≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£ģ

£®1£©Ĺę…Ō√śĶńŐű–őÕ≥ľ∆Õľ≤Ļ≥šÕÍ’Ż£Ľ
£®2£©‘ŕ…»–őÕ≥ľ∆Õľ÷–£¨—°‘Ů°įįģĻķ°Ī÷ųŐ‚ňý∂‘”¶Ķń‘≤–ńĹ« «_____∂»£Ľ
£®3£©»ÁĻŻł√–£∆ŖńÍľ∂Ļ≤”–1200√ŻŅľ…ķ£¨«ŽĻņľ∆—°‘Ů“‘°į”—…∆°Īő™÷ųŐ‚Ķń∆ŖńÍľ∂—ß…ķ”–______√Ż£Ľ
£®4£©—ß…ķĽŠ–Żīę≤Ņ”–∆ŖńÍľ∂Ķń2√Żń–…ķļÕ2√ŻŇģ…ķ£¨Ō÷ī”÷–ňśĽķŐŰ—°2√ŻÕ¨—ß≤őľ”°į÷ųŐ‚’ųőń°Ī–ŻīęĽÓ∂Į£¨«Ž”√ ų◊īÕľ∑®ĽÚŃ–ĪŪ∑®«ů≥Ų«°ļ√—°÷–°į1ń–1Ňģ°ĪĶńłŇ¬ £ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĺō–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() «
«![]() …Ō“Ľ∂ĮĶ„£¨Ķ„
…Ō“Ľ∂ĮĶ„£¨Ķ„![]() «Ķ„
«Ķ„![]() Ļō”ŕ÷ĪŌŖ
Ļō”ŕ÷ĪŌŖ![]() Ķń∂‘≥∆Ķ„£¨‘ŕĶ„
Ķń∂‘≥∆Ķ„£¨‘ŕĶ„![]() Ķń‘ň∂ĮĻż≥Ő÷–”–«“÷Ľ”–“ĽłŲĶ„
Ķń‘ň∂ĮĻż≥Ő÷–”–«“÷Ľ”–“ĽłŲĶ„![]() ĶĹŌŖ∂ő
ĶĹŌŖ∂ő![]() ĶńĺŗņŽő™4£¨‘Ú
ĶńĺŗņŽő™4£¨‘Ú![]() Ķń»°÷Ķ∑∂őß «____________£ģ
Ķń»°÷Ķ∑∂őß «____________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
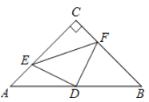
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨“—÷™°ŌC=90°„£¨AC=BC=4£¨D «ABĶń÷–Ķ„£¨Ķ„E,F∑÷Īū‘ŕAC,BC…Ō‘ň∂Į£¨£®Ķ„E≤Ľ”ŽĶ„A,C÷ōļŌ£©£¨«“Ī£≥÷AE=CF£¨Ń¨Ĺ”DE£¨EF£¨‘Ŕīő‘ň∂ĮĪšĽĮĻż≥Ő÷–£¨”–Ō¬Ń–ĹŠ¬Ř£ļĘŔňńĪŖ–őCEDF”–Ņ…ń‹≥…ő™’ż∑Ĺ–ő£ĽĘŕ°ųDFE «Ķ»—Ł÷ĪĹ«»żĹ«–ő£ĽĘŘňńĪŖ–őCEDFĶń√śĽż «∂®÷Ķ£ģ∆š÷–’ż»∑ĶńĹŠ¬Ř «£ļ______________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
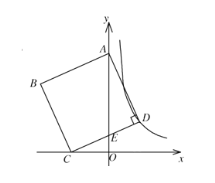
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨’ż∑Ĺ–őABCDĶń√śĽżő™20£¨∂•Ķ„A‘ŕy÷Š…Ō£¨∂•Ķ„C‘ŕx÷Š…Ō£¨∂•Ķ„D‘ŕňę«ķŌŖ![]() ĶńÕľŌů…Ō£¨ĪŖCDĹĽy÷Š”ŕĶ„E£¨»Ű
ĶńÕľŌů…Ō£¨ĪŖCDĹĽy÷Š”ŕĶ„E£¨»Ű![]() £¨‘ÚkĶń÷Ķő™______.
£¨‘ÚkĶń÷Ķő™______.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com