
【题目】阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
【答案】
(1)解:△ADE∽△FCD,理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD
(2)解:由题意知,AD=CD=1,AE= ![]() .
.
在直角△DEA中,有DE= ![]() =
= ![]() =
= ![]() .
.
由(1)可得: ![]() =
= ![]() ,则CF=
,则CF= ![]() =
= ![]()
【解析】(1)利用正方形的性质和平行线的性质,由两角法证明△ADE∽△FCD;
(2)根据勾股定理及相似三角形对应边成比例求解。
【考点精析】关于本题考查的勾股定理的概念和正方形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
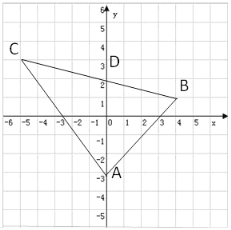
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉揭示了二项和![]() 的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
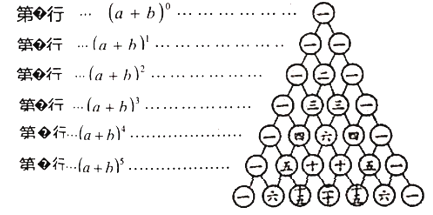
(1)观察“杨辉三角”规律,依次写出“杨辉三角”第![]() 行中从左到右的各数;
行中从左到右的各数;
(2)请运用幂的意义和多项式乘法法则,按如下要求展开下列各式,以验证“杨辉三角”第四行的规律:展开后各项按字母![]() 降幂、
降幂、![]() 升幂排列
升幂排列![]()
(3)解不等式![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根据以上信息,解答下列问题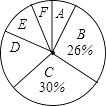
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com