
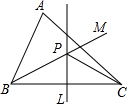
 如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM平分∠ABC,PL与BM相交于点P.若∠A=57°,∠ACP=27°,则∠BCP=32度.
如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM平分∠ABC,PL与BM相交于点P.若∠A=57°,∠ACP=27°,则∠BCP=32度. 分析 根据角平分线定义求出∠ABP=∠CBP,根据线段的垂直平分线性质得出BP=CP,求出∠CBP=∠BCP,根据三角形内角和定理得出方程3∠ABP+21°+60°=180°,求出方程的解即可.
解答 解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=57°,∠ACP=27°,
∴3∠ABP+27°+57°=180°,
解得:∠ABP=32°.
∴∠BCP=32°,
故答案为:32.
点评 本题考查了三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能求出∠ABP=∠CBP=∠BCP是解此题的关键,数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
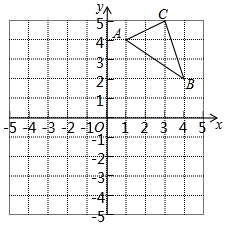 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=0,n为任何实数 | B. | m=0,n>0 | C. | m为任何实数,n=0 | D. | m>0,n=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )
如图,∠ACB=∠CDB=Rt∠,则点B到直线CD的距离等于图中某条线段的长,这条线段是( )| A. | 线段BD | B. | 线段CD | C. | 线段AC | D. | 线段BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com