
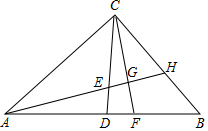
 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )| A. | 2 | B. | π | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$π |
分析 由△ADE≌△CDF,推出∠DAE=∠DCF,因为∠AED=∠CEG,推出∠ADE=∠CGE=90°,推出A、C、G、D四点共圆,推出点G的运动轨迹为弧CD,利用弧长公式计算即可.
解答 解:如图,
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,
∴∠ADE=∠CDF=90°,CD=AD=DB,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDF}\\{DE=DF}\end{array}\right.$,
∴△ADE≌△CDF,
∴∠DAE=∠DCF,
∵∠AED=∠CEG,
∴∠ADE=∠CGE=90°,
∴A、C、G、D四点共圆,
∴点G的运动轨迹为弧CD,
∵AB=4,AB=$\sqrt{2}$AC,
∴AC=2$\sqrt{2}$,
∴OA=OC=$\sqrt{2}$,
∵DA=DC,OA=OC,
∴DO⊥AC,
∴∠DOC=90°,
∴点G的运动轨迹的长为$\frac{90π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
故选D.
点评 本题考查等腰直角三角形的性质、轨迹、勾股定理、全等三角形的判定和性质,四点共圆等知识,解题的关键是正确探究点G的轨迹,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
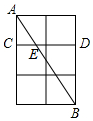 如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.
如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
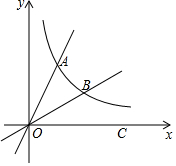 如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.
如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 飞机上升9000米,再上升-5000米,则飞机实际上升4000米 | |
| B. | 一个正数,一个负数,它们表示的意义一定相反 | |
| C. | 0是最小的有理数 | |
| D. | 正数和负数统称为有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com