
分析 根据线段中点的性质,可得AE的长,根据线段的和差,可得答案.
解答 解:如图1 ,
,
由点C为线段AB的中点,得
AC=$\frac{1}{2}$AB=9cm.
由点D为线段AE的中点,且DE=6cm,得
AE=2DE=12cm.
由线段的和差,得
CE=AE+AC=12+9=21cm.
如图2 ,
,
由点C为线段AB的中点,得
AC=$\frac{1}{2}$AB=9cm.
由点D为线段AE的中点,且DE=6cm,得
AE=2DE=12cm.
由线段的和差,得
CE=AE-AC=12-9=3cm,
综上所述:CE的长为21cm或3cm.
点评 本题考查了两点间的距离,利用线段的和差是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
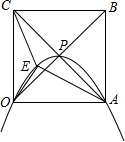 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 租赁时间<1小时 | 免费 |
| 1小时<租赁时间≤2小时 | 1元 |
| 2小时<租赁时间≤3小时 | 2元 |
| 租赁时间>3小时 | 3元/小时(不足1小时按1小时计) |
| 租赁时间≤24小时 | 最高收费30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
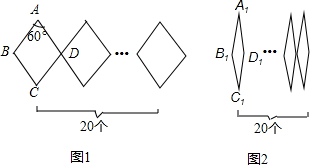
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2400}{x}$=$\frac{2400+30}{x+3}$ | B. | $\frac{2400+30}{x}$=$\frac{2400}{x-3}$ | ||
| C. | $\frac{2400-30}{x-3}$=$\frac{2400}{x}$ | D. | $\frac{2400-30}{x}$=$\frac{2400}{x-3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com