
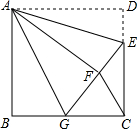
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:分析 根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;由Rt△ABG≌Rt△AFG,可得S△ABG=S△AFG;求得∠GAF=45°,∠AGB+∠AED=180°-∠GAF=135°.
解答 解:∵△AFE是由△ADE折叠得到,
∴AF=AD,∠AFE=∠AFG=∠D=90°,
又∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D,
∴AB=AF,∠B=∠AFG=90°,
在Rt△ABG和Rt△AFG中,
∵$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
故①正确;
∵正方形ABCD中,AB=6,CD=3DE,
∵EF=DE=$\frac{1}{3}$CD=2,
设BG=FG=x,则CG=6-x.
在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,
解得x=3.
∴BG=3,CG=6-3=3;
∴BG=CG;
∴②正确.
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF;
∴③正确
∵Rt△ABG≌Rt△AFG,
∴S△ABG=S△AFG;
∴④正确;
∵∠BAG=∠FAG,∠DAE=∠FAE,
又∵∠BAD=90°,
∴∠GAE=45°,
∴∠AGB+∠AED=180°-∠GAE=135°.
∴⑤错误.
故答案为:4.
点评 此题属于四边形的综合题.考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定等知识.注意折叠中的对应关系,注意掌握方程思想的应用是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )| A. | t>-5 | B. | -5<t<3 | C. | 3<t≤4 | D. | -5<t≤4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
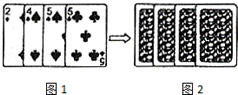 四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=AC=3,BC=6 | B. | ∠A=40°、∠B=70° | ||
| C. | AB=3、BC=8,周长为16 | D. | ∠A=40°、∠B=50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15cm,8cm,7cm | B. | 4cm,5cm,10cm | C. | 4cm,5cm,6cm | D. | 3cm,9cm,6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com