
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
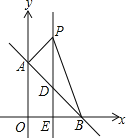
【答案】(1)y=﹣x+4,点B的坐标为(4,0);(2)①2n﹣4;②(2,6);③6,4).
【解析】
(1)把点A的坐标代入直线解析式可求得b=4,则直线的解析式为y=﹣x+4,令y=0可求得x=4,故此可求得点B的坐标;
(2)①由题l垂直平分OB可知OE=BE=2,将x=2代入直线AB的解析式可求得点D的坐标,设点P的坐标为(2,n),然后依据S△APB=S△APD+S△BPD可得到△APB的面积与n的函数关系式为S△APB=2n﹣4;
②由S△ABP=8得到关于n的方程可求得n的值,从而得到点P的坐标;
③如图1所示,过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.设点C的坐标为(p,q),先证明△PCM≌△CBN,得到CM=BN,PM=CN,然后由CM=BN,PM=CN列出关于p、q的方程组可求得p、q的值;如图2所示,同理可求得点C的坐标.
(1)∵把A(0,4)代入y=﹣x+b得b=4
∴直线AB的函数表达式为:y=﹣x+4.
令y=0得:﹣x+4=0,解得:x=4
∴点B的坐标为(4,0).
(2)①∵l垂直平分OB,
∴OE=BE=2.
∵将x=2代入y=﹣x+4得:y=﹣2+4=2.
∴点D的坐标为(2,2).
∵点P的坐标为(2,n),
∴PD=n﹣2.
∵S△APB=S△APD+S△BPD,
∴S△ABP=![]() PDOE+
PDOE+![]() PDBE=
PDBE=![]() (n﹣2)×2+
(n﹣2)×2+![]() (n﹣2)×2=2n﹣4.
(n﹣2)×2=2n﹣4.
②∵S△ABP=8,
∴2n﹣4=8,解得:n=6.
∴点P的坐标为(2,6).
③如图1所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.
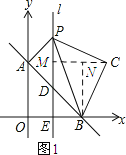
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
![]() ,
,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴![]() ,解得
,解得![]() .
.
∴点C的坐标为(6,4).
如图2所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.
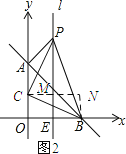
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
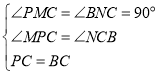 ,
,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴![]() ,解得
,解得![]() .
.
∴点C的坐标为(0,2)舍去.
综上所述点C的坐标为(6,4).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
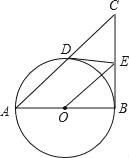
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
(1)证明OE∥AD;
(2)①当∠BAC= °时,四边形ODEB是正方形.
②当∠BAC= °时,AD=3DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
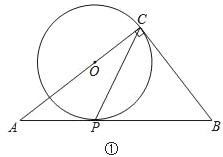
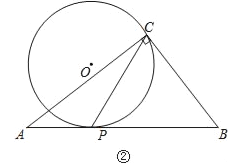
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
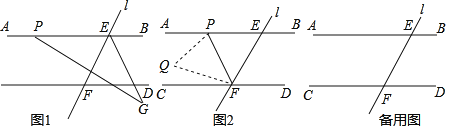
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点)
(1)若∠CFE=119°,PG交∠FEB的平分线EG于点G,∠APG=150°,则∠G的大小为 .
(2)如图2,连接PF.将△EPF折叠,顶点E落在点Q处.
①若∠PEF=48°,点Q刚好落在其中的一条平行线上,请直接写出∠EFP的大小为 .
②若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
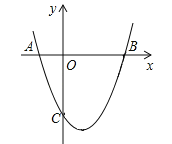
【题目】如图,抛物线与x轴的交点分别为A、B,与y轴的负半轴交于点C.已知抛物线的顶点坐标为(1,﹣4),点B的坐标(3,0).
(1)求该抛物线的解析式.
(2)在该函数图象上能否找到一点P,使PO=PC?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2nx﹣n2+n的顶点为P,直线y=![]() 分别交x,y轴于点M,N.
分别交x,y轴于点M,N.
(1)若点P在直线MN上,求n的值;
(2)是否存在过(0,﹣2)的直线与抛物线交于A,B两点(A点在B点的下方),使AB为定长,若存在,求出AB的长;若不存在,请说明理由;
(3)在(2)的条件下,当四边形MABN的周长最小时,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,同时在甲服装店租用2件和乙服装店租用3件共需280元,在甲服装店租用4件和乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,则超出5件的部分可按原价的六折进行优惠;设需要租用![]() (
(![]() )件服装,选择甲店则需要
)件服装,选择甲店则需要![]() 元,选择乙店则需要
元,选择乙店则需要![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
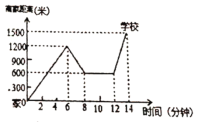
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com