
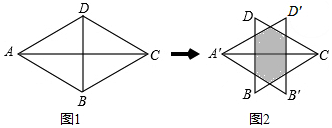
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
分析 根据等边三角形的性质以及平移的性质,即可得到OM+MN+NR+GR+EG+OE=A′D′+CD=2+2=4;根据A′F=$\frac{\sqrt{3}}{2}$,即可得到MO≠MN,进而得出阴影部分不是正六边形;阴影部分的面积=△A′B′D′的面积-△A′MN的面积-△OD′E的面积-△RGB′的面积,据此进行计算即可.
解答 解:∵两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移到△A′B′D′的位置,
∴A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′,
∴OM+MN+NR+GR+EG+OE=A′D′+CD=2+2=4,
故①正确;
∵k=$\frac{\sqrt{3}}{2}$,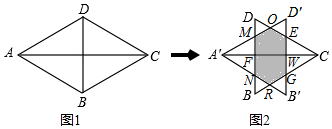
∴A′F=$\frac{\sqrt{3}}{2}$,
∴A′M=A′F÷cos30°=1,MN=1.
∴MO=$\frac{1}{2}$(2-1)=$\frac{1}{2}$.
∴MO≠MN,
∴阴影部分不是正六边形,
故②错误;
阴影部分的面积=△A′B′D′的面积-△A′MN的面积-△OD′E的面积-△RGB′的面积
=$\frac{\sqrt{3}}{4}$×(22-12-2×($\frac{1}{2}$)2]
=$\frac{5\sqrt{3}}{8}$,
故③正确,
故选:C.
点评 本题主要考查了等边三角形的性质以及平移的性质的运用,解决问题的关键是依据平移的距离,得到小等边三角形的边长及面积.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
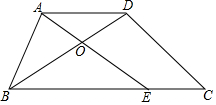 如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm.
如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+5x-1=x(x+5)-1 | B. | x2+3x-4=x(x+3-$\frac{4}{x}$) | C. | x2-9=(x+3)(x-3) | D. | (x+2)(x-2)=(x-2)(x+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 总金额($) | $10 | $5 | $5 | $2 |
| $10 | 20 | 15 | 15 | 12 |
| $5 | 15 | 10 | 10 | 7 |
| $5 | 15 | 10 | 10 | 7 |
| $2 | 12 | 7 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com