
【题目】在矩形纸片ABCD中,AB=6,BC=8.
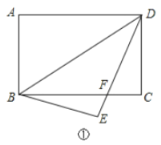
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,求BF的长;
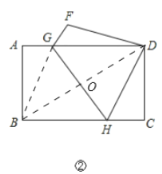
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.

【答案】(1)![]()
(2)![]()
【解析】
(1)根据折叠的性质可得∠ADB=∠EDB,再根据两直线平行,内错角相等可得∠ADB=∠DBC,然后求出∠FBD=∠FDB,根据等角对等边可得BF=DF,设BF=x,表示出CF,在Rt△CDF中,利用勾股定理列出方程求解即可;
(2)根据折叠的性质可得DH=BH,设BH=DH=x,表示出CH,然后在Rt△CDH中,利用勾股定理列出方程求出x,再连接BD、BG,根据翻折的性质可得
(1) 由折叠得,∠ADB=∠EDB,
∵矩形ABCD的对边AD∥BC,
∴∠ADB=∠DBC,
∴∠FBD=∠FDB,
∴BF=DF,
设BF=x,则CF=8x,
在Rt△CDF中,![]()
即![]()
解得x=![]()
故答案:![]()
(2)由折叠得,DH=BH,设BH=DH=x,
则CH=8x,
在Rt△CDH中, ![]()
即![]()
解得x=![]()
连接BD、BG,
由翻折的性质可得,BG=DG,∠BHG=∠DHG,
∵矩形ABCD的边AD∥BC,
∴∠BHG=∠DGH,
∴∠DHG=∠DGH,
∴DH=DG,
∴BH=DH=DG=BG,
∴四边形BHDG是菱形,
在Rt△BCD中,
S菱形BHDG=![]() BDGH=BHCD,
BDGH=BHCD,
即![]() ×10GH=
×10GH=![]() ×6,解得GH=
×6,解得GH=![]() .
.
故答案:![]()


科目:初中数学 来源: 题型:
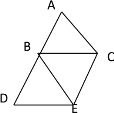
【题目】如图,等边三角形ABC沿边AB方向平移到△BDE的位置,则图中∠CBE=_____,连接CE后,线段CE与AD的关系是______,△BEC为____三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D,E分别是△ABC的BC,AC边的中点.
(1)如图①,若AB=10,求DE的长;
(2)如图②,点F是AB边上的一点,FG//AD,交ED的延长线于点G.求证:AF=DG

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
(1)请你画出它的从正面看和从左面看的形状图.
(2)如果每个立方体的棱长为2cm,则该几何体的表面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
求1+2+22+23+…...+22014的值,另S=1+2+22+23+…...+22014,
等式两边同时乘2,得2S=2+22+23+.......+22014+22015
两式相减,得2S - S = 22015 -1 所以S = 22015 - 1
依据以上计算方法,计算:1 + 3 + 32 + ..... + 32019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 和一次函数
和一次函数![]() 的图象都经过点P(m,-3m).
的图象都经过点P(m,-3m).
(1)求点P的坐标和一次函数的解析式;
(2)若点M(a,y1)和点N(a+1,y2)(a>0)都在反比例函数的图象上,试通过计算或利用反比例的性质,说明y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
(1)求证:E为AC中点;
(2)求证:AD=CD;
(3)若AB=10,cos∠ABC=![]() ,求tan∠DBC的值.
,求tan∠DBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com