
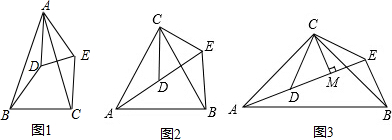
分析 (1)根据全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE.
(2)首先根据△ACB和△DCE均为等边三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为60°即可.
(3)首先根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;最后根据DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可.
解答 (1)证明:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△BAD≌△CAE,
∴BD=CE.
(2)解:∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE,
∴BE=AD,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
综上,可得
∠AEB的度数为60°;线段BE与AD之间的数量关系是:BE=AD.
(3)解:∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD,∠BEC=∠ADC,
∵点A,D,E在同一直线上,
∴∠ADC=180-45=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135-45=90°;
∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
∴AE=AD+DE=BE+2CM.
故答案为:60°、BE=AD.
点评 (1)此题主要考查了全等三角形的判定方法和性质,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件.
(2)此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
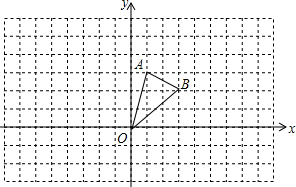 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 手机品牌 | 芒果手机 | 四星手机 | 大米手机 |
| 销售量(台) | 200 | 80 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
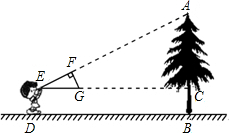 如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )| A. | 5m | B. | 5.5m | C. | 5.6m | D. | 5.8m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某种酸奶中钙的含量 | B. | 了解某班学生的课外作业时间 | ||
| C. | 公司招聘职员,对应聘人员的面试 | D. | 旅客上飞机前的安检 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com