
 ��֪�߶�a����ͼ���������в��軭ͼ��
��֪�߶�a����ͼ���������в��軭ͼ������ ��1��������ֱ��l����ֱ��l����ȡһ��O������Բ����l����Բ������⣻
��2���ȸ�����������ͼ�Σ��ٸ��ݾ��ε��ж���⼴�ɣ�
��3����OΪԲ�ģ��߶�a�ij�Ϊ�뾶����Բ��Ϊ����
��� �⣺��1����ͼ��ʾ�������ĵ���������2����
������ֱ��l����ֱ��l����ȡһ��O������Բ����l����Բ��������⣻
��2����ͼ��ʾ�������ĵ�������4�������˳�����߶ΰ����������������ܵõ����Σ�
��3����ͼ��ʾ����Բ����������O�ľ���Ϊa�����еĵ㣬�������һ��Բ��
���� ��������ͼ-������ͼ�����������Ŀ�Ĺؼ�����Ϥ��������ͼ�ε����ʣ���ϼ���ͼ�εĻ������ʰѸ�����ͼ���ɻ�����ͼ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����κ���y=ax2+bx-3��ͼ����x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C���������ߵĶ���ΪM��
��ͼ�����κ���y=ax2+bx-3��ͼ����x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C���������ߵĶ���ΪM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D������O�İ뾶Ϊ5��AB=8����CD�ij���2��
��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D������O�İ뾶Ϊ5��AB=8����CD�ij���2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵ��߸˵Ķ���A�͵���B��C���㴦��������˿��AB��AC����֪���߸�AD�ij�Ϊ12m��BD�ij�Ϊ9m��DC�ij�Ϊ16m�����˿�ߵ��ܳ���
��ͼ���ڵ��߸˵Ķ���A�͵���B��C���㴦��������˿��AB��AC����֪���߸�AD�ij�Ϊ12m��BD�ij�Ϊ9m��DC�ij�Ϊ16m�����˿�ߵ��ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ͼ�����ı���ABCD�У�AD��BC��BC��AD��BDƽ�֡�ABC��E��F�ֱ���BD��AC���е㣮��֤��
��֪��ͼ�����ı���ABCD�У�AD��BC��BC��AD��BDƽ�֡�ABC��E��F�ֱ���BD��AC���е㣮��֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{16}$=��4 | B�� | 3-2=-$\frac{1}{9}$ | C�� | ��$\sqrt{3}-\sqrt{2}$��2=1 | D�� | ��$\sqrt{2}$-1��0=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
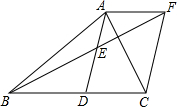 ��֪���ڡ�ABC�У�AD��BC���ϵ����ߣ���E��AD���е㣻����A��AF��BC����BE���ӳ�����F������CF��
��֪���ڡ�ABC�У�AD��BC���ϵ����ߣ���E��AD���е㣻����A��AF��BC����BE���ӳ�����F������CF���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com