
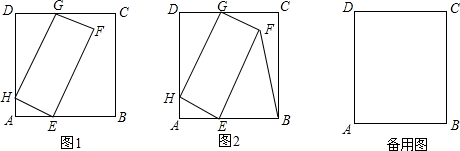
���� ��1����t=1ʱ��DG=2���Ӷ��õ�DG=AH��Ȼ���֤����HDG�ס�EAH�������������ε����ʿ�֪��$\frac{GH}{EH}=\frac{DG}{AH}$���Ӷ��õ�GH=HE������Ϊ�ı���EFGH�Ǿ��Σ��ʴ��ı���EFGH�������Σ�
��2���ɣ�1����֪����HDG�ס�EAH�������������ε����ʿ�֪��$\frac{DG}{DH}=\frac{AH}{AE}$������$\frac{2t}{10}=\frac{2}{8}$���Ӷ������t=$\frac{5}{4}$��
��3����ͼ3��ʾ������F��FM��AB������֤����HDG�ա�FME���Ӷ��õ�DH=FM=12-t��Ȼ����ݡ�DHG�ס�AEH����֪$\frac{DH}{AE}=\frac{DG}{AH}$�������AE=6$-\frac{t}{2}$������BE=4+$\frac{t}{2}$�����������������ε������ʽ�ó�������BEF�������t�ĺ�����ϵʽ�������䷽������õ�t=2ʱ����BEF����������ֵ�����ֵΪ25��
��� �⣺��1����t=1��
��DG=2��
��DG=AH��
���ı���EFGHΪ���Σ�
���GHE=90�㣮
���DHG+��AHE=90�㣮
�ߡ�AHE+��AEH=90�㣬
���DHG=��AEH��
�֡ߡ�D=��A=90�㣬
���HDG�ס�EAH��
��$\frac{GH}{EH}=\frac{DG}{AH}=\frac{2}{2}=1$��
��GH=HE��
�֡��ı���EFGH�Ǿ��Σ�
���ı���EFGH�������Σ�
��2���ɣ�1����֪����HDG�ס�EAH��
��$\frac{DG}{DH}=\frac{AH}{AE}$������$\frac{2t}{10}=\frac{2}{8}$��
���t=$\frac{5}{4}$��
��3����ͼ3��ʾ������F��FM��AB��
�ɣ�1����֪����DHG=��AEH��
�ߡ�AEH+��FEM=90�㣬��FEM+��EFM=90�㣬
���HEA=��EFM��
���DHG=��EFM��
�ڡ�HDG�͡�FME�У�
$\left\{\begin{array}{l}{��D=��EMF=90��}\\{��DHG=��EFM}\\{GH=EF}\end{array}\right.$��
���HDG�ա�FME��
��DH=FM��
��AH=t��DG=2t��
��DH=12-t��
�ɣ�1����֪��DHG�ס�AEH��
��$\frac{DH}{AE}=\frac{DG}{AH}$����$\frac{12-t}{AE}=\frac{2t}{t}$��
��AE=6$-\frac{t}{2}$��
��BE=4+$\frac{t}{2}$
��${S}_{��BEF}=\frac{1}{2}EB•FM=\frac{1}{2}EB•DH$=$\frac{1}{2}����4+\frac{1}{2}t����12-t��$=$-\frac{1}{4}{t}^{2}+t+24$=$-\frac{1}{4}��t-2��^{2}+25$��
�൱t=2ʱ����BEF�����Ϊ25��
���� ������Ҫ����������������ε����ʺ��ж������ε����ʡ�ȫ�������ε����ʺ��ж����䷽������κ�������ֵ���ۺ�Ӧ�ã�֤�á�HDG�ա�FME����DHG�ס�AEH�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{{a}^{2}-1}$ | B�� | $\sqrt{a}$ | C�� | $\sqrt{2a+1}$ | D�� | $\sqrt{{a}^{2}+0.1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪D��E�ֱ��ǵ�AB��AC���ϵĵ㣬DE��BC����AE��EC=2��5����ôS��ADE��S�ı���DBCE����4��21��
��ͼ����֪D��E�ֱ��ǵ�AB��AC���ϵĵ㣬DE��BC����AE��EC=2��5����ôS��ADE��S�ı���DBCE����4��21���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com