
分析 利用$\frac{1}{\sqrt{n}}$=$\frac{2}{\sqrt{n}+\sqrt{n}}$<$\frac{2}{\sqrt{n}+\sqrt{n-1}}$=2($\sqrt{n}$-$\sqrt{n-1}$),$\frac{1}{\sqrt{n}}$=$\frac{2}{\sqrt{n}+\sqrt{n}}$>$\frac{2}{\sqrt{n}+\sqrt{n+1}}$=2($\sqrt{n+1}$-$\sqrt{n}$),利用裂项求和即可得出S的整数部分.
解答 解:∵$\frac{1}{\sqrt{n}}$=$\frac{2}{\sqrt{n}+\sqrt{n}}$<$\frac{2}{\sqrt{n}+\sqrt{n-1}}$=2($\sqrt{n}$-$\sqrt{n-1}$),$\frac{1}{\sqrt{n}}$=$\frac{2}{\sqrt{n}+\sqrt{n}}$>$\frac{2}{\sqrt{n}+\sqrt{n+1}}$=2($\sqrt{n+1}$-$\sqrt{n}$),
∴S=1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{100}}$<1+2($\sqrt{100}$-1)=19,
S=1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{100}}$>1+2($\sqrt{101}$-$\sqrt{2}$)≈18.27,
∴S的整数部分是18.
故答案为:18.
点评 考查了估算无理数的大小,有理化因式,根式求和,裂项求和,放缩法,涉及推理能力与计算能力,难度较大.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
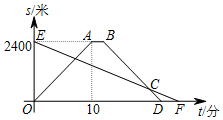 小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com