
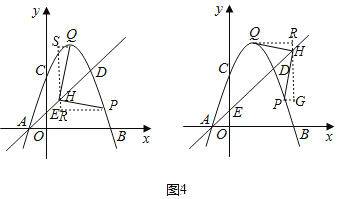
����Ŀ����ͼ��������y��ax2+bx+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C��0��3������OB��OC��3AO��ֱ��y��x+1�������߽���A��D���㣬��y�ύ�ڵ�E����Q�������ߵĶ��㣬��ֱ��AD�Ϸ����������ϵĶ���P�ĺ�����Ϊm��
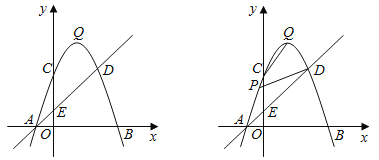
��1����������ߵĽ���ʽ������Q�����ꣻ
��2������CQ���ж��߶�CQ���߶�AE��������ϵ��λ�ù�ϵ����˵�����ɣ�
��3������PA��PD����mΪ��ֵʱ��S��PAD��![]() S��DAB��
S��DAB��
��4����ֱ��AD���Ƿ����һ��Hʹ��PQHΪ����ֱ�������Σ������������m��ֵ����������˵�����ɣ�
���𰸡���1��y����x2+2x+3�� Q��1��4������2���߶�CQ���߶�AE��������ϵ��λ�ù�ϵ��ƽ������ȣ����������������3��m��0��1����4�����ڣ�m��0��2��1![]() ��
��
��������
��1��ֱ��y��x+1�������߽���A�㣬���A����1��0������E��0��1�������B��C������ֱ�Ϊ����3��0������0��3����������⣻
��2��CQ��![]() ��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����������⣻
��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����������⣻
��3��S��PAD��![]() ��PK����xD��xA����
��PK����xD��xA����![]() ��3������m2+2m+3��m��1����
��3������m2+2m+3��m��1����![]() S��DAB��
S��DAB��![]() ��4��3��������⣻
��4��3��������⣻
��4���֡�QOH��90������PQH��90������QHP��90������������ֱ���⼴�ɣ�
��1��ֱ��y��x+1�������߽���A�㣬���A����1��0������E��0��1����
���B��C������ֱ�Ϊ����3��0������0��3����
�������ߵı���ʽΪ��y��a��x+1����x��3����a��x2��2x��3����
����3a��3����ã�a����1��
�������ߵı���ʽΪ��y����x2+2x+3��
�����ĶԳ���Ϊ��x��1���ʵ�Q��1��4����
��2��CQ��![]() ��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����
��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����
���߶�CQ���߶�AE��������ϵ��λ�ù�ϵ��ƽ������ȣ�
��3������ֱ��y��x+1�������ߵı���ʽ����ã�x��0��2���ʵ�D��2��3����
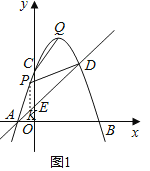
����P��y���ƽ���߽�AD�ڵ�K��
���P��m����m2+2m+3�������K��m��m+1����
S��PAD��![]() ��PK����xD��xA����
��PK����xD��xA����![]() ��3������m2+2m+3��m��1����
��3������m2+2m+3��m��1����![]() S��DAB��
S��DAB��![]() ��4��3��
��4��3��
��ã�m��0��1��
�ʵ�P��0��3����1��4����
��4�����ڣ����ɣ�
���H��t��t+1������P��m��n����n����m2+2m+3������Q��1��4����
�ٵ���QOH��90��ʱ����ͼ1��
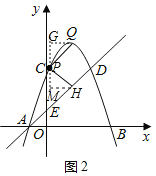
����O��y���ƽ���ߣ��ֱ���H����Q��x���ƽ�����ڵ�M��G��
�ߡ�GQP+��QPG��90������QPG+��HPM��90�������HPM����GQP��
��PGQ����HMP��90����PH��PQ��
���PGQ�ա�HMP��AAS������PG��MH��GQ��PM��
����4��n��t��m��1��m��n��t��1��
��ã�m��0��2��
�ʵ�P��2��3����0��3����
�ڵ���PQH��90��ʱ��
���QHP����QPH��45������PH��x�ᣬ
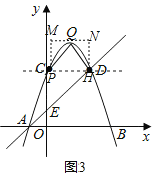
ͬ���ɵã�m��0��2��
�ʵ�P��2��3����0��3����
�۵���QHP��90��ʱ��
����H�ڵ�D���·�ʱ�������ͼ��
ͬ���ɵã�m��3��
�ʵ�P��3��0����
����H�ڵ�D���·�ʱ�����Ҳ�ͼ��
ͬ���ɵã�m��1![]() ��
��
�ʵ�P��1+![]() ��2����1��
��2����1��![]() ��2����
��2����
���ϣ���P������Ϊ����2��3����0��3����3��0����1+![]() ��2����1��
��2����1��![]() ��2����
��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
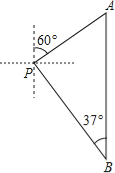
����Ŀ��С��һ����һ���������棬��������һ�µ��������ڹµ�P���ۿ�С����ְ��ں��л�������ͼ��ʾ����С����P���������ر�ƫ��60��������200��A�������������Ϸ�����һ��ʱ�䵽B������B��С���۲�������ڵ�P���ڱ�ƫ��37���ķ����ϣ���ʱС���������������ף���ȷ��1�ף���
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
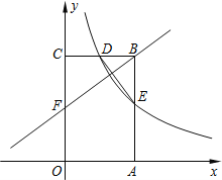
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ![]() ��˫����
��˫����![]() ��ͼ��BC���е�D������AB���ڵ�E������DE��
��ͼ��BC���е�D������AB���ڵ�E������DE��
��1����k��ֵ����E�����ꣻ
��2������F��OC����һ�㣬����FBC�ס�DEB����ֱ��FB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չ��ѧ�����ʵ�����������������������������������ͨ�ල����־Ը�߶��飬ÿ��ѧ�����ѡ��һ�����飬Ϊ���˽�ѧ����ѡ�����������ȡA��B��C��D�ĸ��࣬��200��ѧ�����е��飮������õ������ݽ������������Ƴ�����ͳ��ͼ����������

��1��������ͳ��ͼ�н�ͨ�ල�������ε�Բ�ĽǶ�����
��2����D��ѡ��������ѧ������������ȫ����ͳ��ͼ������ܰ��ʾ���뻭�ڴ�������Ӧ��ͼ�ϣ�
��3������У����ѧ��2500�ˣ��Թ��Ƹ�Уѡ������������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
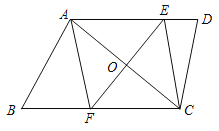
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����O�ǶԽ���AC���е㣬����O��AC�Ĵ��ߣ��ֱ�AD��BC�ڵ�E��F������AF��CE��
��1����֤����AOE�ա�COF��
��2�����ж��ı���AFCE����״����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ�����ѧ������Ȥ�����齨������ȤС�飬�������ȡ�˲���ͬѧ����Ȥ���ý��е��飬���ռ����������������Ƴ���������ͳ��ͼ�������ͼ�е���Ϣ������������⣺
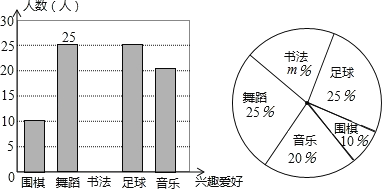
![]() ѧУ��ε��鹲��ȡ�� ��ѧ����
ѧУ��ε��鹲��ȡ�� ��ѧ����
![]() ��
��![]() ��ֵ����ȫ����ͳ��ͼ��
��ֵ����ȫ����ͳ��ͼ��
![]() ������ͳ��ͼ�У���Χ�����������ε�Բ�ĽǶ���Ϊ ��
������ͳ��ͼ�У���Χ�����������ε�Բ�ĽǶ���Ϊ ��
![]() ���У����ѧ��
���У����ѧ��![]() ����������Ƹ�У�ж�����ѧ��ϲ������
����������Ƹ�У�ж�����ѧ��ϲ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ�����ҹ��������ĵ���֮һ��ɽ�����ҵ����Ϊֹ����![]() �������ʷ.����������ʷ�����У�ɽ�����������Ʒ�ַ��ࡢ������������Ƽ��������Էھơ���Ҷ�����Ϊ����.ij�̾Ƴ���������Ҷ��ƣ�ÿƿ�ɱ�����
�������ʷ.����������ʷ�����У�ɽ�����������Ʒ�ַ��ࡢ������������Ƽ��������Էھơ���Ҷ�����Ϊ����.ij�̾Ƴ���������Ҷ��ƣ�ÿƿ�ɱ�����![]() Ԫ�������鷢�֣����ۼ�Ϊ
Ԫ�������鷢�֣����ۼ�Ϊ![]() Ԫʱ��ÿ������۳�
Ԫʱ��ÿ������۳�![]() ƿ���ۼ�ÿ����
ƿ���ۼ�ÿ����![]() Ԫ���ɶ��۳�
Ԫ���ɶ��۳�![]() ƿ���ۼ۲�����
ƿ���ۼ۲�����![]() Ԫ��
Ԫ��
��1���ۼ�Ϊ����ʱ����ʹÿ������������������Ƕ��٣�
��2��Ҫʹÿ���������![]() Ԫ��ÿƿ��Ҷ��Ƶ��ۼ�Ӧ�ÿ�����ʲô��Χ�ڣ�
Ԫ��ÿƿ��Ҷ��Ƶ��ۼ�Ӧ�ÿ�����ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x�ᡢy���ϣ�OA��4��OC��3��ֱ��m��y����![]() x��ԭ��O��������x����������ÿ��1����λ���ȵ��ٶ��˶�����ֱ��m�����OABC�����߷ֱ��ڵ�M��N��ֱ��m�˶���ʱ��Ϊt(��)�����OMN�����ΪS�����ܷ�ӳS��t֮�亯����ϵ�Ĵ���ͼ����(����)
x��ԭ��O��������x����������ÿ��1����λ���ȵ��ٶ��˶�����ֱ��m�����OABC�����߷ֱ��ڵ�M��N��ֱ��m�˶���ʱ��Ϊt(��)�����OMN�����ΪS�����ܷ�ӳS��t֮�亯����ϵ�Ĵ���ͼ����(����)

A. 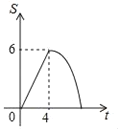 B.
B. 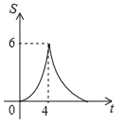 C.
C.  D.
D. 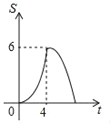
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������Բ��O��BC��CA��AB�ֱ������ڵ�D��E��F����AB=13��BC=15��CA=14����tan��EDF��ֵΪ�� ��
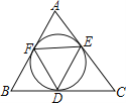
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com