
【题目】关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为正,求实数m的取值范围?
【答案】解:∵关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为正,∴a=1,b=2,c=1﹣2m,1﹣2m>0,
∴m< ![]() ,
,
∴b2﹣4ac=4﹣4(1﹣2m)=8m≥0,即m≥0,
∴m 的取值范围为:0≤m< ![]()
【解析】根据根与系数的关系可得1﹣2m>0,然后此方程有两个实数根可知△≥0,即可求得m的取值范围.
【考点精析】根据题目的已知条件,利用根与系数的关系的相关知识可以得到问题的答案,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


科目:初中数学 来源: 题型:
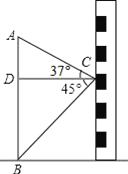
【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)﹣8﹣6+22﹣9.
(2)(﹣![]() +
+![]() ﹣
﹣![]() )×48.
)×48.
(3)|﹣0.75|+(﹣3)﹣(﹣0.25)+|﹣![]() |+
|+![]() .
.
(4)﹣22+3×(﹣1)4﹣(﹣4)×5.
(5)(7m2n﹣5mn)﹣(4m2n﹣5mn)
(6)![]() (9a﹣3)+2(a+1).
(9a﹣3)+2(a+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图16,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=![]()
![]() +k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.
+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y= ![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.图象经过点(﹣1,5)
B.图象分布在第二、四象限
C.当x>0时,y随x增大而增大
D.当x<0时,y随x增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com