
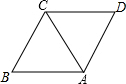
 如图,在菱形ABCD中,对角线AC=4,∠B=60°,则菱形ABCD面积为8$\sqrt{3}$.
如图,在菱形ABCD中,对角线AC=4,∠B=60°,则菱形ABCD面积为8$\sqrt{3}$. 分析 根据菱形的性质可得BA=BC,BD⊥AC,AO=CO=$\frac{1}{2}$AC=,2,BO=DO=$\frac{1}{2}$BD,然后证明△ABC是等边三角形,可得BC=AC,再利用勾股定理求出BO长,进而可得BD长,然后根据菱形的面积公式进行计算即可.
解答 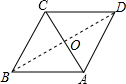 解:连接BD,交AC于O,
解:连接BD,交AC于O,
∵四边形ABCD是菱形,
∴BA=BC,BD⊥AC,AO=CO=$\frac{1}{2}$AC=,2,BO=DO=$\frac{1}{2}$BD,
∵∠B=60°,
∴△ABC是等边三角形,
∴BC=AC=4,
∵BD⊥AC,
∴∠CBO=30°,
∴BO=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$
∴BD=4$\sqrt{3}$,
∴菱形ABCD面积为:$\frac{1}{2}$•AC•BD=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$,
故答案为:8$\sqrt{3}$.
点评 此题主要考查了菱形的性质,关键是掌握菱形的菱形的四条边都相;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 9800名学生是总体 | B. | 每个学生是个体 | ||
| C. | 100名学生是所抽取的一个样本 | D. | 样本容量是100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
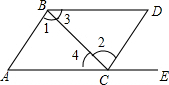 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
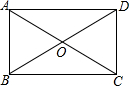 如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )
如图,在矩形ABCD中,已知AB=4,OA=3,则BC的长度为( )| A. | 5 | B. | $2\sqrt{5}$ | C. | $2\sqrt{13}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.
如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
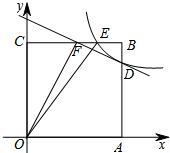 如图,正方形OABC的边长为4,反比例函数y=$\frac{k}{x}$(k>0)的图象与线段AB交于点D,与线段BC交于点E,点E的坐标为(3,4).
如图,正方形OABC的边长为4,反比例函数y=$\frac{k}{x}$(k>0)的图象与线段AB交于点D,与线段BC交于点E,点E的坐标为(3,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com