

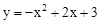 (2)(1,2)(3)存在,(
(2)(1,2)(3)存在,(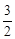 ,
, )
)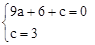 ,解得
,解得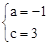 。
。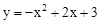 。
。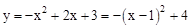 ,∴对称轴为x=1。
,∴对称轴为x=1。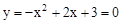 ,解得x1=3,x2=-1,∴C(-1,0)。
,解得x1=3,x2=-1,∴C(-1,0)。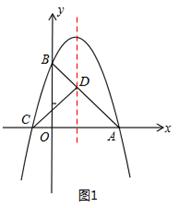
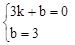 ,解得
,解得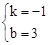 。
。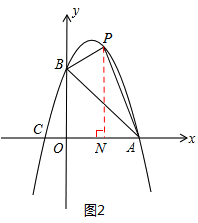

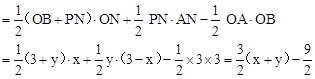
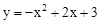 ,代入上式得:
,代入上式得: 。
。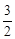 时,S△ABP取得最大值。
时,S△ABP取得最大值。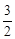 时,
时,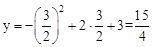 ,∴P(
,∴P(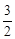 ,
, )。
)。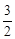 ,
, )。
)。

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 。
。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
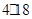 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度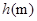 与飞行时间
与飞行时间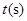 的关系式是
的关系式是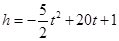 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A.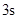 | B.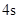 | C.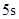 | D.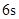 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com