
【题目】如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.

(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由
【答案】(1)抛物线的解析式:y=﹣x2+2x+3;(2)MN=﹣m2+3m(0<m<3);(3)存在,当m=![]() 时,△BNC的面积最大为
时,△BNC的面积最大为![]() .
.
【解析】
(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)设MN交x轴于D,那么![]() 的面积可表示为:
的面积可表示为:![]() ,MN的表达式在(2)中已求得,OB的长易知,由此列出关于
,MN的表达式在(2)中已求得,OB的长易知,由此列出关于![]() 的函数关系式,即可得出结论.
的函数关系式,即可得出结论.
解:
(1)设![]()
则 
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
(2)设直线BC的解析式为![]()
则![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
已知点M的横坐标为![]() ,
,
∴![]() ,
,
![]() ,
,
(3)

如图可知:![]() ,
,
![]()
=![]()
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
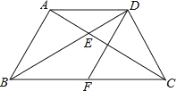
【题目】如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:![]() ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组为测量如图(①所示的一段古城墙的高度,设计用平面镜测量的示意图如图②所示,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处。

(1)已知AB⊥BD、CD⊥BD,且测得AB=1.2m,BP=1.8m.PD=12m,求该城墙的高度(平面镜的原度忽略不计):
(2)请你设计一个测量这段古城墙高度的方案。
要求:①面出示意图(不要求写画法);②写出方案,给出简要的计算过程:③给出的方案不能用到图②的方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=3,OC=6![]() ,则另一直角边BC的长为_____.
,则另一直角边BC的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O与点E,连接BE,CE.

(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为______时,四边形AOCE是菱形;
②若AE=![]() ,AB=2
,AB=2![]() ,则DE的长为______.
,则DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第8个图形的小圆个数是( )
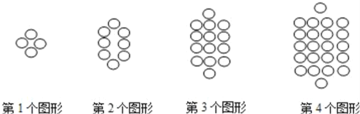
A.58B.66C.74D.80
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com