
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 是
是![]() 的中点,
的中点,![]() 于
于![]() 交
交![]() 于
于![]() 交
交![]() 的延长线于
的延长线于![]() .
.
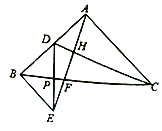
求证: (1)![]() ;
;
(2) ![]() 垂直平分
垂直平分![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据ASA即可证明△DBP≌△EBP;
(2)想办法证明△DBP≌△EBP(SAS)即可解决问题;
证明:(1)由题意可知,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,
∴∠DAH=∠ACH,
∵∠BAC=90°,BE∥AC,
∴∠CAD=∠ABE=90°.
又∵AB=CA,
∴在△ABE与△CAD中,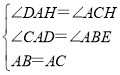
∴△ABE≌△CAD(ASA).
(2)∵△ABE≌△CAD,
∴AD=BE,
又∵AD=BD,
∴BD=BE,
在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,
故∠ABC=45°.
∵![]() ,
,
∴∠ABE=90°,
∴∠EBF=90°45°=45°,
∴△DBP≌△EBP(SAS),
∴DP=EP,
即可得出BC垂直且平分DE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)如图所示,现有下列四个结论:①abc>0 ②b2-4ac<0 ③c<4b ④a+b>0.其中正确的结论有( )

A. 1个 B. 3个 C. 2个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
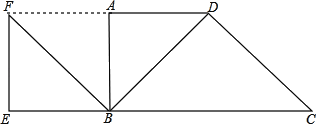
【题目】在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°,∠C=( )
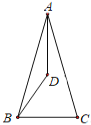
A.50°B.65°C.80°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
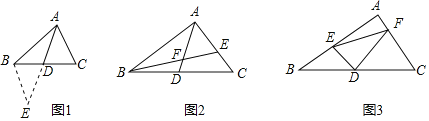
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com