
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:
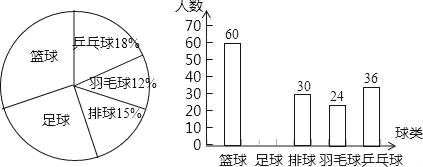
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取 名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“足球”所对应的圆心角的度数;
(3)该校共有3000名学生,请估计全校学生喜欢足球运动的人数.
(4)甲乙两名学生各选一项球类运动,请求出甲乙两人选同一项球类运动的概率.
【答案】(1)200;(2)详见解析;(3)750;(4)![]() .
.
【解析】
(1)用排球的人数÷排球所占的百分比,即可求出抽取学生的人数;
(2)足球人数=学生总人数-篮球的人数-排球人数-羽毛球人数-乒乓球人数,即可补全条形统计图;
(3)计算足球的百分比,根据样本估计总体,即可解答;
(4)利用概率公式计算即可.
(1)30÷15%=200(人).
答:共抽取200名学生进行问卷调查;
故答案为200.
(2)足球的人数为:200﹣60﹣30﹣24﹣36=50(人),“足球球”所对应的圆心角的度数为360°×0.25=90°.
如图所示:
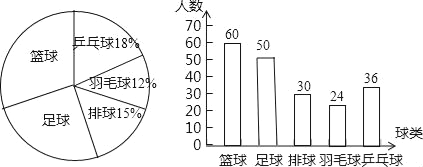
(3)3000×0.25=750(人).
答:全校学生喜欢足球运动的人数为750人.
(4)画树状图为:(用A、B、C、D、E分别表示篮球、足球、排球、羽毛球、乒乓球的五张卡片)

共有20种等可能的结果数,其中小雷和小正两人中有且只有一人选中自己喜欢的项目的结果数为4,
所以小雷和小正两人中有且只有一人选中自己喜欢的项目的概率P(A)=![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止.甲、乙两车相距的路程
地,两车分别到达目的地后停止.甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时,![]() ,
,![]() .
.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲车到达距![]() 地70千米处时,求甲、乙两车之间的路程.
地70千米处时,求甲、乙两车之间的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
(I)计算△ABC的边AC的长为_____.
(II)点P、Q分别为边AB、AC上的动点,连接PQ、QB.当PQ+QB取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段PQ、QB,并简要说明点P、Q的位置是如何找到的_____(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() 。
。

(1)求点![]() 到
到![]() 轴的距离;
轴的距离;
(2)连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,猜想线段![]() 和线段
和线段![]() 的数量关系,并说明理由。
的数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD平分∠ABF,且交AE于点D.
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习等边三角形时发现了直角三角形的一个性质:直角三角形中,![]() 角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在
角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在![]() 中,
中,![]() ,则:
,则:![]() .
.
探究结论:(1)如图1,![]() 是
是![]() 边上的中线,易得结论:
边上的中线,易得结论:![]() 为________三角形.
为________三角形.
(2)如图2,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是边
是边![]() 上任意一点,连接
上任意一点,连接![]() ,在
,在![]() 边上方作等边
边上方作等边![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间的数量关系,写出你的猜想加以证明.
之间的数量关系,写出你的猜想加以证明.
拓展应用:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上的一动点,以
轴正半轴上的一动点,以![]() 为边作等边
为边作等边![]() ,当点
,当点![]() 在第一象内,且
在第一象内,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
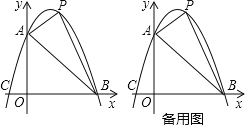
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.

已知:如图,钝角∠AOB.求作:∠AOB的角平分线.
作法:

①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() 的长为半径作弧,在∠AOB内,两弧交于点C;
的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程:
由①可得:OD=OE
由②可得:_________________
由③可知:OC=OC
∴______≌_________(依据:________________________)
∴可得∠COD=∠COE(全等三角形对应角相等)
即OC就是所求作的∠AOB的角平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com