
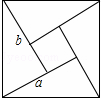
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为 .
科目:初中数学 来源: 题型:
下列运算正确的是( )
|
| A. | ﹣2(a﹣1)=﹣2a﹣1 | B. | (﹣2a)2=﹣2a2 | C. | (2a+b)2=4a2+b2 | D. | 3x2﹣2x2=x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图:在▱ABCD中,AC为其对角线,过点D作AC的平行线与BC的延长线交于E.
(1)求证:△ABC≌△DCE;
(2)若AC=BC,求证:四边形ACED为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
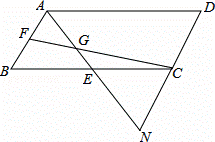
如图,在▱ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB=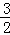 GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,4),抛物线y=﹣x2+mx+n经过点A和C.

(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为S1,右侧部分图形的面积记为S2,求S1与S2的比.
(3)在y轴上取一点D,坐标是(0,),将直线OC沿x轴平移到O′C′,点D关于直线O′C′的对称点记为D′,当点D′正好在抛物线上时,求出此时点D′坐标并直接写出直线O′C′的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com