
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
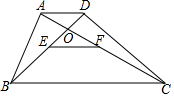 四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).
四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.
小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com