
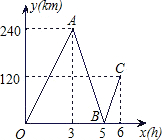
 行驶的时间为x(h),两船之间的距离为y(km),图中的折线表示y与x之间的函数关系.
行驶的时间为x(h),两船之间的距离为y(km),图中的折线表示y与x之间的函数关系.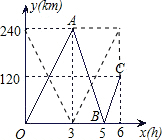 解:(1)从图中可知,两船首次相遇需要5小时;
解:(1)从图中可知,两船首次相遇需要5小时; ,解得
,解得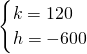 ,
, ,解得
,解得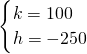 ,
,

 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
 行驶的时间为x(h),两船之间的距离为y(km),图中的折线表示y与x之间的函数关系.
行驶的时间为x(h),两船之间的距离为y(km),图中的折线表示y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 | 3 |
 发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?
发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 倍,前去追赶乙货轮,问乙货轮出
倍,前去追赶乙货轮,问乙货轮出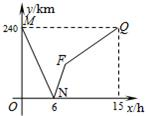 发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?
发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?查看答案和解析>>
科目:初中数学 来源:2009年河南省新乡市中考数学模拟试卷(1)(解析版) 题型:解答题
 倍,前去追赶乙货轮,问乙货轮出发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?
倍,前去追赶乙货轮,问乙货轮出发多长时间被巡逻艇追上(巡逻艇折返的时间忽略不计)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com