
分析 各方程整理为一般形式,找出a,b,c的值,代入求根公式即可求出解.
解答 解:(1)这里a=1,b=-2,c=-8,
∵△=4+32=36,
∴x=$\frac{2±6}{2}$,
解得:x1=4,x2=-2;
(2)这里a=1,b=2,c=-4,
∵△=4+16=20,
∴x=$\frac{-2±2\sqrt{5}}{2}$=-1±$\sqrt{5}$;
(3)这里a=2,b=-3,c=2,
∵△=9-16<0,
∴此方程无解;
(4)方程整理得:9x2-6x+1=0,
这里a=9,b=-6,c=1,
∵△=36-36=0,
∴x=$\frac{2±6}{2}$,
∴此方程解为x1=x2=$\frac{1}{3}$;
(5)方程整理得:3x2-x-2=0,
这里a=3,b=-1,c=-2,
∵△=1+24=25,
∴x=$\frac{1±5}{6}$,
解得:x1=1,x2=-$\frac{2}{3}$;
(6)这里a=1,b=-2$\sqrt{2}$,c=2,
∵△=8+8=16,
∴x=$\frac{2\sqrt{2}±4}{2}$=$\sqrt{2}$±2,
解得:x1=$\sqrt{2}$+2,x2=$\sqrt{2}$-2.
点评 此题考查了解一元二次方程-公式法,熟练掌握求根公式是解本题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
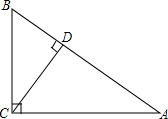 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1\frac{9}{16}}$=$\frac{5}{4}$ | B. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | C. | $\sqrt{0.25}$=0.05 | D. | -$\sqrt{-49}$-(-7)=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com