
分析 (1)根据一元二次方程的根与系数的关系,以及x1+2x2=0,求得m的值;
(2)y轴平分三角形CPQ面积,P,Q横坐标互为相反数,则把一次函数解析式代入二次函数解析式得到的一元二次方程的两个解的根的和是0,据此即可求解.
解答 解:(1)∵x1+x2=m-4,x1+2x2=0
∴x2=4-m
x1=2m-8
∵x1•x2=-(2m+4)=(4-m)(2m-8)
∴m=2或7,
∵x1<x2,即2m-8<4-m,
∴m<3,
∴m=2.
则抛物线的解析式是:y=-x2-2x+8;
(2)∵y轴平分三角形CPQ面积,
∴P,Q横坐标互为相反数
联立方程$\left\{\begin{array}{l}{y=-{x}^{2}-2x+8}\\{y=kx+b}\end{array}\right.$,
则x2+(2+k)x+b-8=0,
∵x1+x2=-(2+k)=0,
△=(2+k)2-4(b-8)>0,
解得:k=-2,b<8.
点评 本题考查了二次函数与一元二次方程,二次函数与x轴的交点的横坐标就是对应的方程的根.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:单选题
一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是是( )
A. 第一次右拐60°,第二次左拐120°
B. 第一次左拐60°,第二次右拐60°
C. 第一次左拐60°,第二次左拐120°
D. 第一次右拐60°,第二次右拐60°
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:判断题
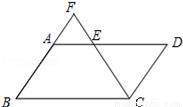
已知:如图,平行四边形ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
求证:AB=AF.
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:单选题
一元二次方程4x2+1=4x的根的情况是( )
A. 没有实数根 B. 只有一个实数根
C. 有两个相等的实数根 D. 有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
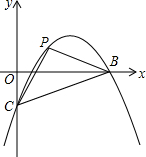 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A,B,与y轴交于点C,点P为抛物线上一点,且△PBC的内外圆的圆心在x轴上,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
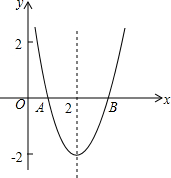 已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.
已知抛物线y=a(x-2)2+c如图所示,该抛物线与x轴交于A,B两点,点B的坐标为($\sqrt{7}$,0),试求方程a(x-2)2+c=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
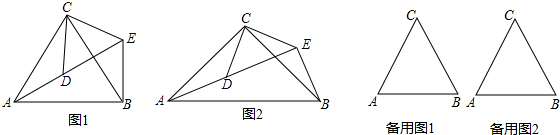
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com