
【题目】如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.

(1)求证:△CEB≌△ADC;
(2)若AD=9cm,BE=3cm,求DE的长.
【答案】(1)证明见解析;(2)DE= 6.
【解析】试题分析: (1)由同角的余角相等可得∠BCE=∠CAD,而BC=AC,∠E=∠CDA=90°,故有△CEB≌△ADC;
(2)由(1)知BE=DC,CE=AD,从而可求DE的长.
试题解析:(1)∵BE⊥CE于E,AD⊥CE于D,∠ACB=90°,
∴∠E=∠ADC=90°,∠BCE=90°-∠ACD,∠CAD=90°-∠ACD,∴∠BCE=∠CAD,
在△BCE与△CAD中,∠E=∠ADC,∠BCE=∠CAD,BC=AC,
∴△CEB≌△ADC(AAS);
(2)∵△CEB≌△ADC,∴BE=DC=3,CE=AD=9,∴DE=CE-CD=6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于![]() GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
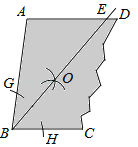
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A.a>1
B.a≤2
C.1<a≤2
D.1≤a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动,设运动时间为t,那么当t=_________秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小明做游戏:一个不透明的袋子中装有6个完全一样的球,每个球上分别标有1,2,2,3,4,5,从袋中任意摸出一个球,然后放回.规定:若摸到的球上所标数字大于3,则小颖赢,否则小明赢.你认为这个游戏公平吗?为什么?如果不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若收入60元记作+60元,则-20元表示( )
A.收入20元B.收入40元C.支付40元D.支付20元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com