
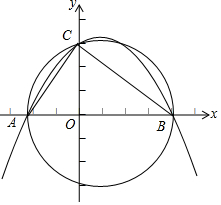
 如图已知A(-$\frac{9}{4}$,0),C(0,3),B为x轴中正半轴上的点,以AB为直径的圆过C点.
如图已知A(-$\frac{9}{4}$,0),C(0,3),B为x轴中正半轴上的点,以AB为直径的圆过C点.分析 (1)根据以AB为直径的圆过C点可得,AB为圆的直径,进而得到∠ACB=90°;
(2)通过判定△AOC∽△BOC,根据OC2=OA•OB,求得B(4,0),再把 A、B的坐标分别代入抛物线y=ax2+bx+3,得 a和b的值,进而得到抛物线的解析式;
(3)当△BOD为等腰三角形时,有OD=OB、BD=BO或DO=DB这三种可能,需要分三种情况讨论:①当OD=OB时,不可能;②当OD=DB时,可得D的坐标为$(2,\frac{3}{2})$;③当BD=BO时,可得D($\frac{4}{5}$,$\frac{12}{5}$).
解答 解:(1)∵AB为圆的直径,
∴∠ACB=90°;
(2)如图,∵∠ACB=90°,CO⊥AB,
∴∠AOC=∠BOC=90°,且∠A=∠BCO,
∴△AOC∽△BOC,
∴$\frac{OC}{OB}=\frac{OA}{OC}$,
∴OC2=OA•OB,
∵A(-$\frac{9}{4}$,0),C(0,3),
∴$AO=\frac{9}{4}$,OC=3,
∴${3^2}=\frac{9}{4}OB$,
∴OB=4,
∴B(4,0),
把 A、B的坐标分别代入抛物线y=ax2+bx+3,得
${(-\frac{9}{4})^2}a-\frac{9}{4}b+3=0$,42a+4b+3=0,
联立方程组后解得:
$a=-\frac{1}{3}$,$b=\frac{7}{12}$,
∴抛物线的解析式为:$y=-\frac{1}{3}{x^2}+\frac{7}{12}x+3$;
(3)如图,当△BOD为等腰三角形时,有OD=OB、BD=BO或DO=DB这三种可能,
分三种情况讨论:
①当OD=OB时,
∵OC=3,OB=4,而D在BC上,
∴OD<OB,
∴OD=OB没有可能;
②当OD=DB时,
如图,过D作DH⊥OB于H,则H 是OB 中点.
由DH∥CO,可得:
$OH=\frac{1}{2}BO=\frac{1}{2}×4=2$,
$DH=\frac{1}{2}OC=\frac{1}{2}×3=\frac{3}{2}$,
∴D的坐标为$(2,\frac{3}{2})$;
③当BD=BO时,
如图,过D作DG⊥OB于G,
∵Rt△BOC中,OB=4,OC=3,
∴由勾股定理可得,BC=5,
而BD=BO=4,
∴CD=5-4=1,
由DG∥CO得:$\frac{OG}{OB}=\frac{CD}{BC}$,即$\frac{OG}{4}=\frac{1}{5}$,
∴$OG=\frac{4}{5}$,
由DG∥CO得:$\frac{DG}{OC}=\frac{BD}{BC}$,即$\frac{DG}{3}=\frac{4}{5}$,
∴$DG=\frac{12}{5}$,
∴D($\frac{4}{5}$,$\frac{12}{5}$).
点评 本题属于二次函数综合题,主要考查了相似三角形的判定与性质、等腰三角形的性质、平行线分线段成比例定理以及勾股定理的综合应用,解题时需要根据圆周角的性质求出角的度数,用待定系数法求出抛物线的解析式,根据等腰三角形的性质确定点D的坐标.解答此题的关键是画出图形,作出辅助线,结合等腰三角形进行分类讨论.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个数之差一定小于被减数 | B. | 减去一个负数,差一定大于被减数 | ||
| C. | 减去一个正数,差一定大于被减数 | D. | 0减去任何数,差都是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | -7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 1.1 | 1.2 | 1.3 | 1.4 |
| ax2+bx+c | -0.59 | 0.84 | 2.29 | 3.76 |
| A. | 1.0<x<1.1 | B. | 1.1<x<1.2 | C. | 1.2<x<1.3 | D. | 1.3<x<1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com