
 在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$.
在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$. 分析 以AB为腰作等腰Rt△ABE,连接EC,由△ADC为等腰Rt△知$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$、∠EAB=∠DAC=45°,结合∠EAB+∠BAC=∠BAC+∠DAC即∠EAC=∠DAB,证△EAC∽△BAD得$\frac{BD}{EC}$=$\frac{\sqrt{2}}{2}$,作EF⊥BC交BC延长线于F,知∠EBF=30°,从而求得EF=BEsin30°=$\frac{\sqrt{3}}{2}$,FB=BEcos30°=$\frac{3}{2}$,继而得EC=$\sqrt{E{F}^{2}+F{C}^{2}}$=$\sqrt{31}$,根据BD=$\frac{\sqrt{2}}{2}$EC可得答案.
解答 解:以AB为腰作等腰Rt△ABE,连接EC,
∵△ADC为等腰Rt△,
∴$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴$\frac{BD}{EC}$=$\frac{\sqrt{2}}{2}$,
作EF⊥BC交BC延长线于F,
∵∠ABC=60°,∠EBA=90°,
∴∠EBF=30°,
∴EF=BEsin30°=$\frac{\sqrt{3}}{2}$,FB=BEcos30°=$\frac{3}{2}$,
∴EC=$\sqrt{E{F}^{2}+F{C}^{2}}$=$\sqrt{31}$,
∴BD=$\frac{\sqrt{2}}{2}$EC=$\frac{\sqrt{62}}{2}$,
故答案为:$\frac{\sqrt{62}}{2}$.
点评 本题主要考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等重要知识点,有一定难度.正确作出辅助线是本题的难点.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:2017届江苏省无锡市九年级3月月考数学试卷(解析版) 题型:判断题
某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
查看答案和解析>>
科目:初中数学 来源:2017届辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:单选题
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=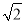 AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
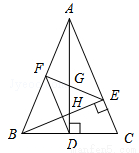
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
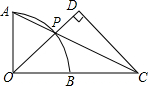 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com